Class 20 (Sampling)

What is Sampling?

Sampling is the process of converting a continuous-time signal into a discrete time signal.

Sampling is accomplished by multiplying a continuous-time signal $x(t)$ with an impulse train, a periodic sequence of impulses with a fundamental period $T_s$ such that $$ \delta_{T_s}(t) = \sum_{k=-\infty}^{\infty} \delta(t - k T_s) \; . $$ We will use the notation $\delta_{T_s}(t)$ to represent a pulse train with sampling period $T_s$. When we multiply $x(t)$ and $\delta_{T_s}(t)$, we get an new train of impulses with amplitudes taken from $x(t)$. Mathematically, we get $$ x_s(t) = x(t) \delta_{T_s}(t) = \sum_{k=-\infty}^{\infty} x(k T_s) \delta(t - k T_s) \; . $$ The question address in the rest of this class is: does the sampling process uniquely preserve all information about our signal?

Fourier Series/Transform of an impulse train

To answer this question, we look at the Fourier series/transform of the impulse train. Since $\delta_{T_s}(t)$ is periodic, we use the Fourier series. When we plug $\delta_{T_s}(t)$ into the Fourier analysis equation, we get $$c_k = \frac{1}{T_s} \int_{T_s} \delta_{T_s}(t) e^{-j k \omega_s t} dt \; .$$ Over one period, $\delta_{T_s}(t)$ is just an impulse. Therefore, the Fourier analysis equation simplifies to $$\begin{eqnarray*} c_k &=& \frac{1}{T_s} \int_{-T_s/2}^{T_s/2} \delta(t) e^{-j k \omega_s t} dt \\ &=& \frac{1}{T_s} (1) \end{eqnarray*}$$ We refer to $\omega_s = 2 \pi / T_s$ as the [angular] sampling frequency.

Since the Fourier series coefficients are defined by $c_k = \frac{1}{T_s}$, the Fourier transform has a value of $2 \pi / T_{s}$ (the $2 \pi$ is introduced because we are in the angular frequency domain) at $k$ times the fundamental angular frequency, i.e. $k \omega_s = k 2 \pi / T_s$, where $k$ is an any integer. Therefore, in the continuous-frequency, we get a pulse train with spacing of $\omega_s$, $$\begin{eqnarray*} \delta_{T_s}(t) &\stackrel{\mathcal{F}}{\longleftrightarrow}& \frac{2 \pi}{T_s} \delta_{\omega_s}(\omega) \\ \end{eqnarray*}$$ Therefore, the Fourier transform of an infinite pulse train with period $T_s$ (i.e., $\delta_{T_s}(t))$ is a infinite pulse train with spacing $\omega_s = 2 \pi / T_s$ (i.e., $({2 \pi}/{T_s}) \delta_{\omega_s}(\omega)$).

Apply multiplication property

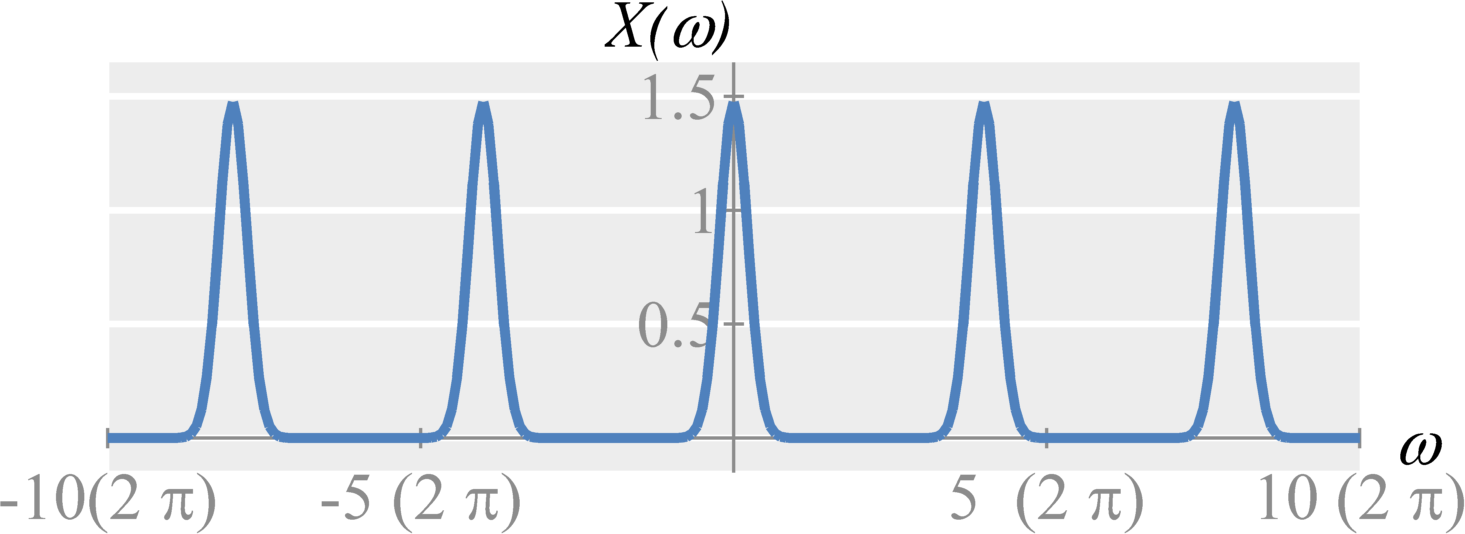
To determine the Fourier transform of $x(t) \delta_{T_s}(t)$, we apply the multiplication property. That is, multiplication in time is equivalent to convolution in frequency. We get the relationship $$\begin{eqnarray*} x(t) \delta_{T_s}(t) &\stackrel{\mathcal{F}}{\longleftrightarrow}& \frac{1}{2 \pi} \left[ X(\omega) * \left( \frac{2 \pi}{T_s} \delta_{\omega_s}(\omega) \right) \right] \\ x(t) \delta_{T_s}(t) &\stackrel{\mathcal{F}}{\longleftrightarrow}& \frac{1}{T_s} \sum_{k=-\infty}^{\infty} X(\omega - k \omega_s) \end{eqnarray*}$$ Therefore, sampling in time results in the sum of shifted replicas of the frequency domain representation $X(\omega)$.

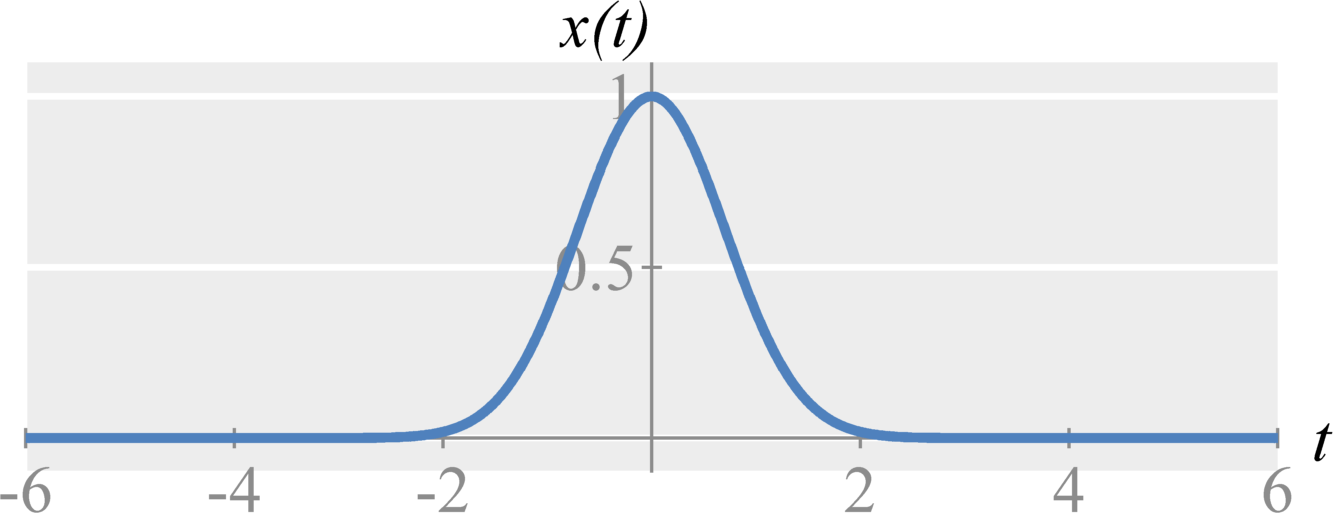
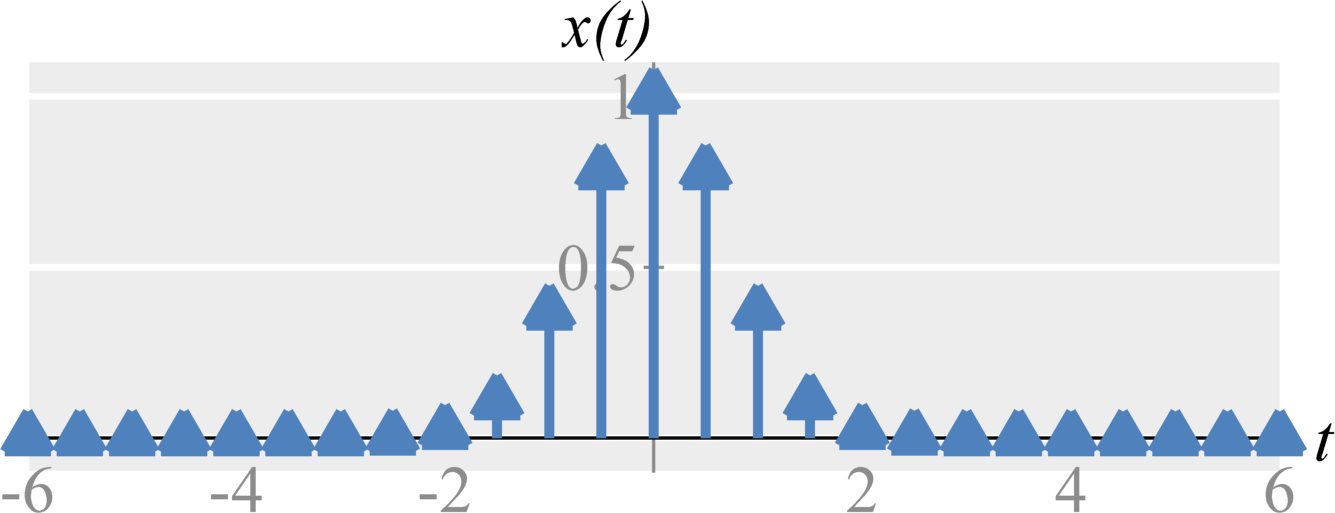
The sampling theorem

We can now answer our question, does the sampling process uniquely preserve all information about our signal? The answer is: yes, but under certain conditions.

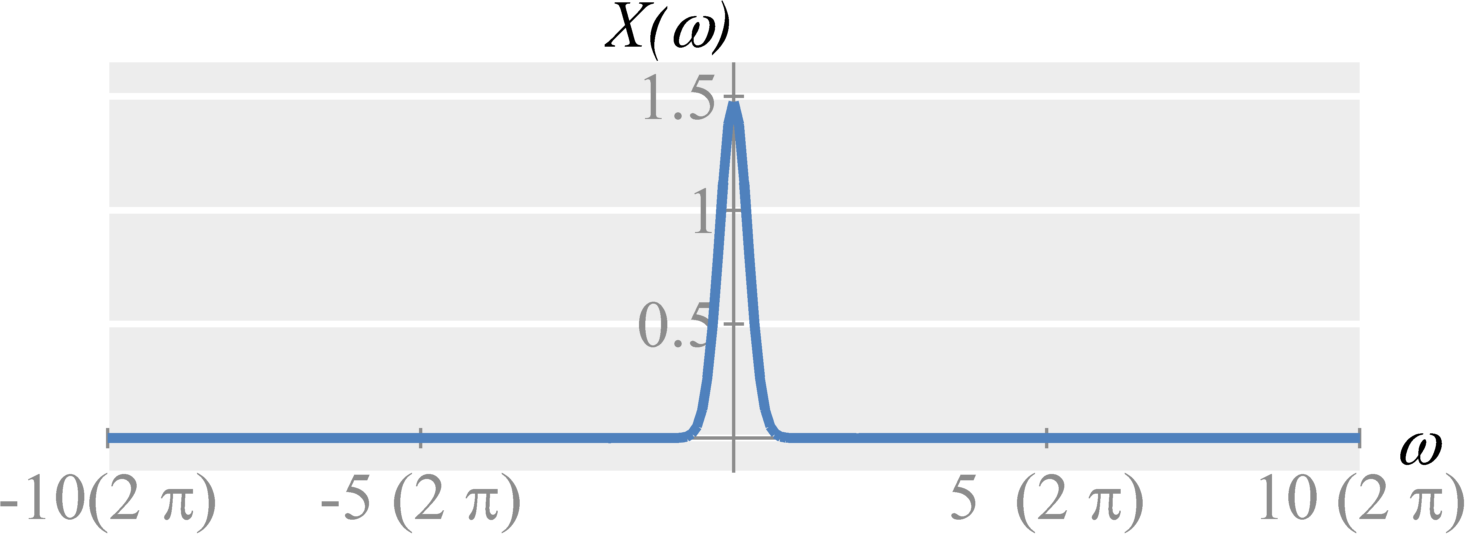
Let the Fourier transform of $x(t)$ be $X(\omega)$ with a largest angular frequency $\omega_{max}$. That is $$X(\omega) = 0 \quad \textrm{for} \quad |\omega| > \omega_{max} \; .$$ Also, let $X_{s}(\omega)$ be defined as the Fourier transform of the sampled signal $x_s(t) = x(t) \delta_{T_s}(t)$ such that $$X_{s}(\omega) = \frac{1}{T_s} \sum_{k=-\infty}^{\infty} X(\omega - k \omega_s) \; .$$

If the bandwidth of the $X(\omega)$, $X(\omega-\omega_s)$, and $X(\omega+\omega_s)$ never overlap, then the original frequency information is remains changed. That is, to preserve all information about the original signal, we require $$\omega_s \geq 2 \omega_{max}$$ or, equivalently, $$\begin{eqnarray*} f_s &\geq& 2 f_{max} \\ T_s &\leq& \frac{1}{2 f_{max}} \\ T_s &\leq& \frac{\pi}{\omega_{max}} \end{eqnarray*} \; .$$ Therefore, the sampling frequency, or sampling rate, must be two times larger than the maximum frequency in the signal. This is known as the sampling theorem or sampling criteria. The frequency $2 f_{max}$ or $2 \omega_{max}$ is known as the Nyquist sampling rate.