Class 10 (Big picture, continuous-time Fourier series)

Representations and Bases

An important concept from signal processing is that we can often uniquely and completely represent a signal as a weighted sum (or weighted integral) of others signals. Mathematiclly, we can write this as $$ x(t) = \sum_{m = \mathcal{M}} c_{m} \phi_{m}(t) \; .$$ The notation $m = \mathcal{M}$ denotes that we are summing over some signal collection (which could be finite or infinite in size). As an integral equation, this would be represented by $$ x(t) = \int_{\mathcal{M}} c(w) \phi(t,w) \; dw \; .$$ If any signal of interest (with properties defined by us) can be uniquely represented by a weighted collection of $\phi_{m}(t)$ or $\phi(t,w)$ functions, then that collection of signals is known as a basis.

Identity Representations

From the sampling theorem, we previously demonstrated that we could represent any signal by a sum of delayed impulses, i.e. $$x(t) = \int_{-\infty}^{\infty} x(\tau) \delta(t-\tau) d\tau .$$ or $$x[n] = \sum_{m=-\infty}^{\infty} x[m] \delta(n-m) .$$ The collection of every $\delta(\tau-t)$ or $\delta(n-m)$ function for $\infty < t,m < -\infty$ is a basis for any signal. This basis is known as the identify basis because the weights $c(\tau) = x(\tau)$ and $c_{m} = x[m]$ are identitcal to original signal.

Frequency Representations

In the rest of this course, we will learn about six closely related representations and bases -- (1) the frequency (Fourier) representation for continuous power signals, (2) the frequency (Fourier) representation for continuous energy signals, (3) the Laplace representation for general continuous signals, (4) the frequency (Fourier) representation for discrete energy signals, (5) the frequency (Fourier) representation for discrete power signals, and (6) the Z representation for general discrete signals.

In these notes, we descibe the frequency representation for continuous power signals -- also known as the Fourier Series representation.

Power Signals

Given any continuous-time, periodic (power) signal $x(t)$ with fundamental period $T_0$ and fundamental angular frequency $\omega_0$, we can represent that signal as a summation of weighted harmonic cosine and sine waves with frequencies equal to integer multiples of the fundamental angular frequency $\omega_0$. Based on this description, we can represent any periodic signal $x(t)$ by $$ \begin{eqnarray} x(t) &=& \sum_{k=0}^{\infty} a_k \cos(k \omega_0 t) + b_k \sin(k \omega_0 t) \\ &=& a_0 + \sum_{k=1}^{\infty} a_k \cos(k \omega_0 t) + b_k \sin(k \omega_0 t) \end{eqnarray} $$ Given this representation, we need to define two operations: synthesis (creating a signal $x(t)$ from frequency coefficients $a_k$ and $b_k$) and analysis (determining the frequency coefficients $a_k$ and $b_k$ from a given signal $x(t)$).

Fourier Series (cosines/sines)

The continuous-time Fourier Series synthesis is defined by $$x(t) = a_0 + \sum_{k=1}^{\infty} a_k \cos(k \omega_0 t) + \sum_{k=1}^{\infty} b_k \sin(k \omega_0 t) $$

Continuous-time Fourier Series analysis is defined by $$a_0 = \frac{1}{T_0} \int_{T_0} x(t) dt$$ $$a_k = \frac{2}{T_0} \int_{T_0} x(t) \cos(k \omega_0 t) dt \quad , \quad k \geq 1$$ $$b_k = \frac{2}{T_0} \int_{T_0} x(t) \sin(k \omega_0 t) dt \quad , \quad k \geq 1$$ where $\omega_0 = 2 \pi / T_0$.

Complex Exponentials

The cosine/sine Fourier Series representation is a bit cumbersome (i.e., there are two sets of coefficients). To condense this representation, we can replace the cosine and sine at each frequency by a complex exponential $$ e^{j \omega t} = \cos(\omega t) + j \sin(\omega t) \; .$$ The complex exponential allows us to represent any weighted cosines and sines using weighted complex exponentials (with complex weights). For example, $$ \begin{eqnarray} (1 - 2j) e^{-j \omega t} + (1 + 2j) e^{+j \omega t} &=& \left[ \left( \cos(\omega t) - j \sin(\omega t) \right) - \left( - 2 j \cos(\omega t) - 2 \sin(\omega t) \right) \right] \\ &\quad& + \left[ \left( \cos(\omega t) + j \sin(\omega t) \right) + \left( - 2 j \cos(\omega t) + 2 \sin(\omega t) \right) \right] \\ &=& 2 \cos(\omega t) + 4 \sin(\omega t) \end{eqnarray} $$ As a result, we can now represent any periodic (power) signal by the simpler expression $$x(t) = \sum_{k=-\infty}^{\infty} c_k e^{j k \omega_0 t } \; .$$

Fourier Series (Complex Exponentials)

We can express the Fourier Series in a more compact manner with complex exponentials. In this case, continuous-time Fourier Series synthesis is defined by $$x(t) = \sum_{k=-\infty}^{\infty} c_k e^{j k \omega_0 t }$$

Continuous-time Fourier Series analysis is defined by $$c_k = \frac{1}{T_0} \int_{T_0} x(t) e^{-j k \omega_0 t} dt$$ where $\omega_0 = 2 \pi / T_0$ and $T_0$ is the fundamental period of the wave.

Existence and convergence

The Fourier Series of a continuous-time, periodic signal $x(t)$ is guaranteed to exist if $$\frac{1}{T_0} \int_{T_0} |x(t)| dt < \infty$$ This is known as the weak Dirchlet condition. Note that if the signal $x(t)$ is a power signal, it will satisfy this property.

The Fourier Series converges to $x(t)$ (i.e. it reconstructs $x(t)$ perfectly) when three conditions are satisfied: $$\frac{1}{T_0} \int_{T_0} |x(t)| dt < \infty$$ $$\text{Finite number of maxima of minima over one period }T$$ $$\text{Finite number of discontinuities over one period }T$$ These are known as the strong Dirchlet conditions.

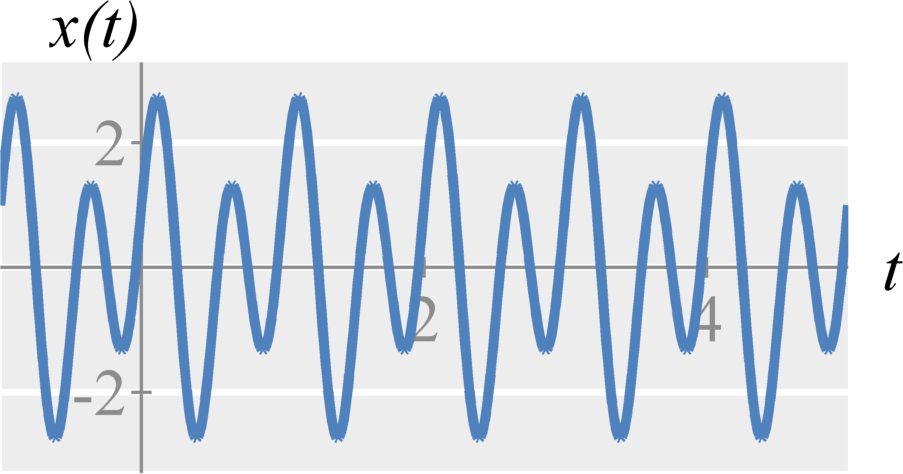
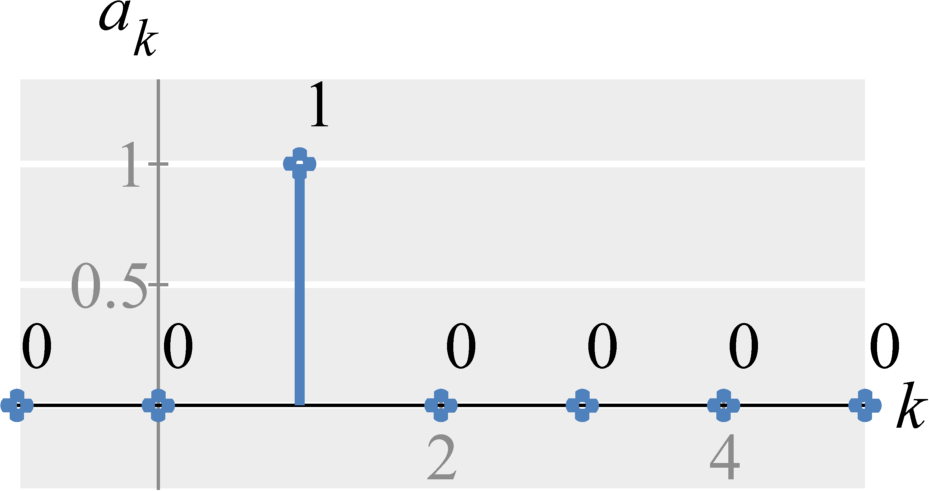
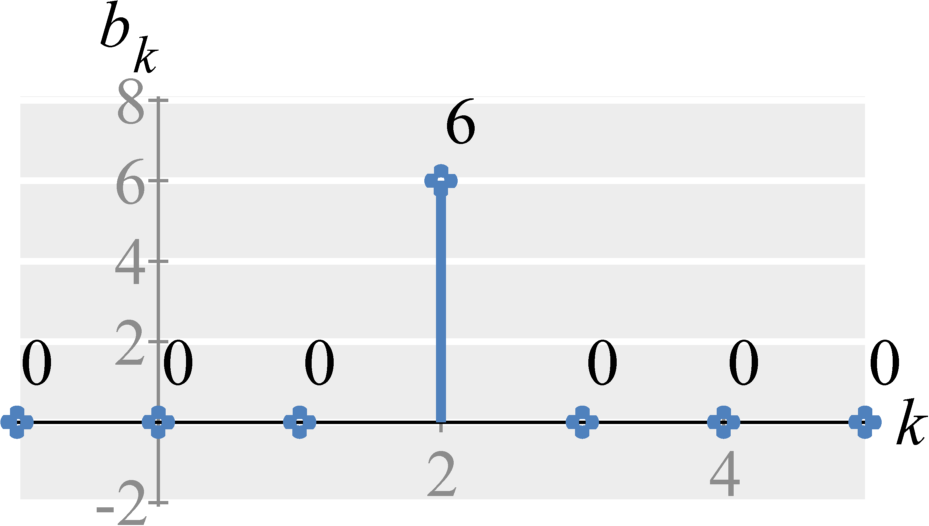
Sine and cosine (Trignometric Fourier Series)

Question: Compute the Fourier components $a_k$ and $b_k$ (using the cosine and sine Fourier series) of $$x(t) = \cos(2 \pi t) + 2 \sin(4 \pi t)$$

Solution: The fundamental period is $T_0 = 1$ and therefore $\omega_0 = 2 \pi$. The frequencies in this signal are $\omega = 2 \pi$ and $\omega = 4 \pi$. So, the harmonics in the Fourier series include the first harmonic (for cosines) and the second harmonic (for sines) .

Mathematically, $$ \begin{eqnarray} a_0 &=& \frac{1}{T_0} \int_{T_0} \cos(2 \pi t) + 2 \sin(4 \pi t) dt \\ &=& 0 + 0 &=& 0 \\ a_1 &=& \frac{2}{T_0} \int_{0}^{1} (\cos(2 \pi t) + 2 \sin(4 \pi t))\cos((1) 2 \pi t) \; dt \\ &=& \frac{2}{1} \int_{0}^{1} \cos(2 \pi t) \cos((1) 2 \pi t) + 2 \sin(4 \pi t) \cos((1) 2 \pi t) \; dt \\ &=& 2 \int_{0}^{1} \cos(2 \pi t) \cos(2 \pi t) + 0 \; dt \\ &=& 2 \int_{0}^{1} \cos^2(2 \pi t) \; dt \\ &=& (\text{Power of } \sqrt{2} \cos(2 \pi t)) \\ &=& \frac{2}{2} = 1 \\ b_1 &=& \frac{2}{T_0} \int_{0}^{1} (\cos(2 \pi t) + 2 \sin(4 \pi t))\sin((1) 2 \pi t) \; dt \\ &=& \frac{2}{1} \int_{0}^{1} \cos(2 \pi t) \sin((1) 2 \pi t) + 2 \sin(4 \pi t) \sin((1) 2 \pi t) \; dt \\ &=& 0 \\ b_2 &=& \frac{2}{T_0} \int_{0}^{1} (\cos(2 \pi t) + 2 \sin(4 \pi t)) \sin((2) 2 \pi t) \; dt \\ &=& \frac{2}{1} \int_{0}^{1} \cos(2 \pi t) \sin((1) 4 \pi t) + 2 \sin(4 \pi t) \sin((1) 4 \pi t) \; dt \\ &=& 2 \int_{0}^{1} 0 + 2 \sin(4 \pi t) \sin(4 \pi t) \; dt \\ &=& \int_{0}^{1} 4 \sin^2(4 \pi t) \; dt \\ &=& (\text{Power of } \sqrt{4} \sin(4 \pi t)) \\ &=& \frac{4}{2} = 2 \end{eqnarray} $$ Hence, $a_0 = 0, a_1 = 1, b_2 = 2$ and all other coefficients are $0$

Verify: If we plug these coefficients into the Fourier series synthesis $$ \begin{eqnarray} x(t) &=& \frac{1}{2}a_0 + \sum_{k=1}^{\infty} a_k \cos(k \omega_0 t) + \sum_{k=1}^{\infty} b_k \sin(k \omega_0 t) \\ &=& \frac{1}{2}a_0 + a_1 \cos((1) \omega_0 t) + b_2 \sin((2) \omega_0 t) \\ &=& \cos( \omega_0 t) + 2 \sin(2 \omega_0 t) \end{eqnarray} $$ This is what we started with. Therefore, our analysis was correct.

Minimal math approach: Notice that the subscripts $k$ of $a_k$ and $b_k$ refer to the harmonic of the sine and cosine values. The frequency of each cosine and sine is $k \times \omega_0$. The values of the coefficients refer to the amplitudes at those harmonics. Therefore, $2 \sin(2 \omega_0 t)$ becomes $b_2 = 2$ and $\cos(1 \omega_0 t)$ becomes $a_1 = 1$.

Sine and cosine (Complex Exponential Fourier Series)

Question: Compute the Fourier components $c_k$ (using complex exponential Fourier series) of $$x(t) = \cos(2 \pi t) + 2 \sin(2 \pi t)$$

Solution: The fundamental period is $T_0 = 1$ and therefore $\omega_0 = 2 \pi$. The only frequency in this signal is $\omega = 2 \pi$. Therefore, the only harmonic in the Fourier series is the first harmonic.

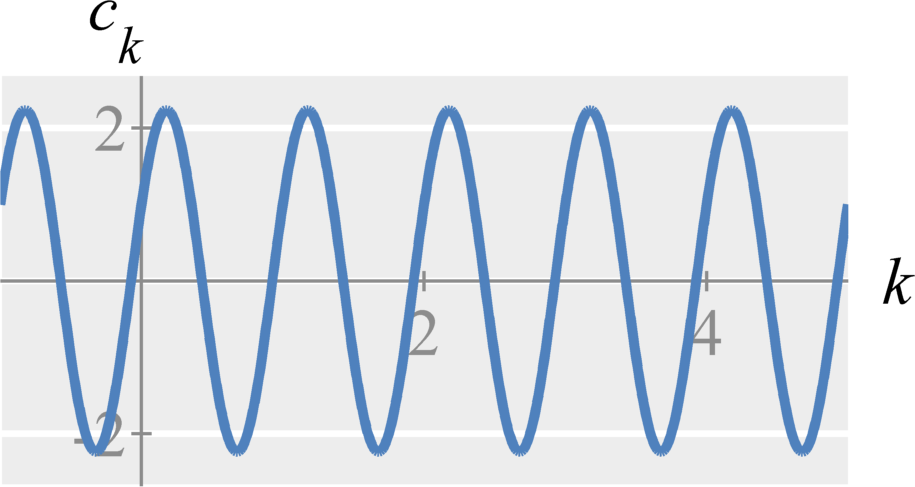
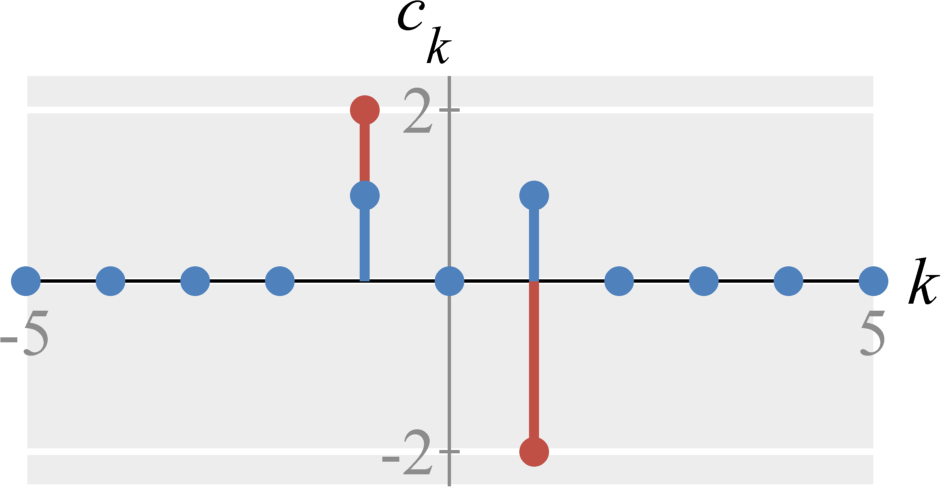
Therefore, $$ \begin{eqnarray} c_0 &=& \frac{1}{T_0} \int_{T_0} \cos(2 \pi t) + 2 \sin(2 \pi t) dt \\ &=& 0 \\ c_1 &=& \int_{0}^{1} (\cos(2 \pi t) + 2 \sin(2 \pi t)) e^{- j (1) 2 \pi t} \; dt \\ &=& \int_{0}^{1} (\cos(2 \pi t) + 2 \sin(2 \pi t)) \left( \cos(2 \pi t) - j \sin(2 \pi t) \right) \; dt \\ &=& \int_{0}^{1} \cos^2(2 \pi t) - j 2 \cos(2 \pi t) \sin(2 \pi t) + \cos(2 \pi t) \sin(2 \pi t) - j 2 \sin(2 \pi t) \sin(2 \pi t) \; dt \\ &=& \int_{0}^{1} \cos^2(2 \pi t) - j 2 \sin^2(2 \pi t) \; dt \\ &=& \frac{1}{2} - j = \frac{1}{2} + \frac{1}{j}\\ c_{-1} &=& \int_{0}^{1} (\cos(2 \pi t) + 2 \sin(2 \pi t)) e^{- j (-1) 2 \pi t} \; dt \\ &=& \int_{0}^{1} (\cos(2 \pi t) + 2 \sin(2 \pi t)) \left( (\cos(2 \pi t) + j \sin(2 \pi t) ) \right) \; dt \\ &=& \int_{0}^{1} \cos^2(2 \pi t) + j 2 \cos(2 \pi t) \sin(2 \pi t) + \cos(2 \pi t) \sin(2 \pi t) + j 2 \sin(2 \pi t) \sin(2 \pi t) \; dt \\ &=& \int_{0}^{1} \cos^2(2 \pi t) + j 2 \sin^2(2 \pi t) \; dt \\ &=& \frac{1}{2} + j = \frac{1}{2} - \frac{1}{j}\\ \end{eqnarray} $$ Hence, $c_0 = 0, c_1 = \frac{1}{2} - j, c_{-1} = \frac{1}{2} + j$ and all other coefficients are $0$

Verify: If we plug these coefficients into the Fourier series synthesis $$ \begin{eqnarray} x(t) &=& \sum_{k=-\infty}^{\infty} c_k e^{j k 2 \pi t } \\ &=& c_{-1} e^{j 2 \pi t } + c_{-1} e^{- j 2 \pi t } \\ &=& \left(\frac{1}{2} - j \right) e^{j 2 \pi t } + \left( \frac{1}{2} + j \right) e^{- j 2 \pi t } \\ \\ &=& \frac{1}{2} \left( e^{j 2 \pi t } + e^{- j 2 \pi t } \right) - j \left( e^{j 2 \pi t } - e^{- j 2 \pi t } \right) \\ &=& \frac{1}{2} \left( e^{j 2 \pi t } + e^{- j 2 \pi t } \right) + \frac{1}{j} \left( e^{j 2 \pi t } - e^{- j 2 \pi t } \right) \\ &=& \cos(2 \pi t) + 2 \sin(2 \pi t) \end{eqnarray} $$ This is what we started with. Therefore, our analysis was correct.

Minimal math approach: Notice that the subscripts $k$ of $c_k$ still refer to the harmonic of the sine and cosine values. The values of the coefficients $c_{k}$ and $c_{-k}$ refer to the half-amplitudes at those harmonics (but possibly a different sign). When the signal is a cosine, the coefficients are real and even. When the signal is a sine, the coefficients are imaginary and odd (and the amplitude at $c_{k}$ is the negative of the coefficient amplitude). Therefore, $2 \sin(2 \omega_0 t)$ becomes $c_{2} = -j$ and $c_{-2} = j$. Also, $\cos(1 \omega_0 t)$ becomes $c_{1} = 1$ and $c_{-1} = 1$ .

Square Wave

Question: Compute the Fourier components $c_k$ (using the complex exponential Fourier series) of a periodic signal with a single period of $$ x(t) = \left\{ \begin{array}{l l} 1 &\;,\;& \textrm{if} \; -1/2 \leq t < 1/2 \\ 0 &\;,\;& \textrm{if} \; 1/2 \leq t < 3/2 \\ \end{array} \right. \\ $$

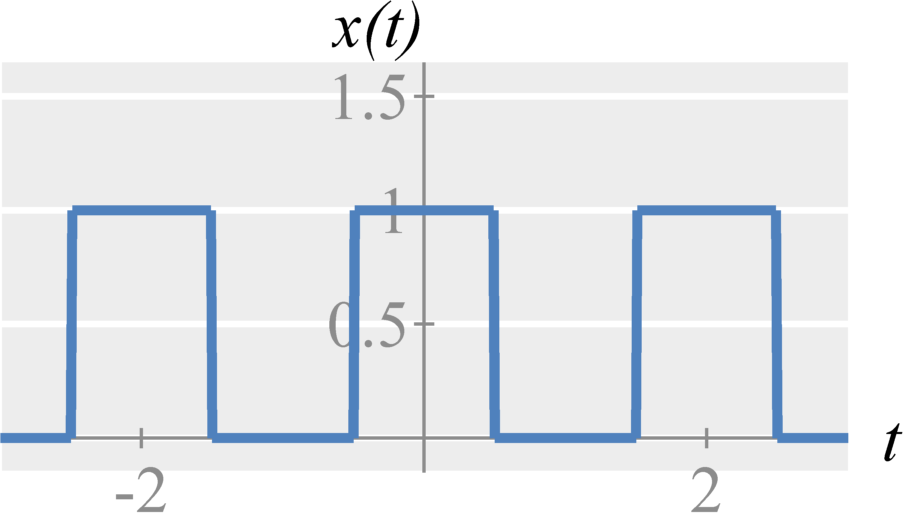
Solution: The fundamental period $T_0 = 2$ and therefore $\omega_0 = \pi$.

We can use the Fourier Series for fundamental frequeny $\omega_0 = 2$ to analysis equation for any $c_k$. $$ \begin{eqnarray} c_k &=& \frac{1}{T_0} \int_{T_0} x(t) e^{j k \omega t} \; dt \\ &=& \frac{1}{2} \int_{-1/2}^{3/2} x(t) e^{j k \pi t} \; dt \\ \end{eqnarray} $$ First, we solve for $k=0$ separately since the integral is fundamentally different than for any other $k$. $$ \begin{eqnarray} c_0 &=& \frac{1}{2} \int_{-1/2}^{3/2} x(t) e^{j (0) 2 \pi t} \; dt \\ &=& \frac{1}{2} \int_{-1/2}^{1/2} 1 \; dt \\ &=& \frac{1}{2} \left. t \right|_{-1/2}^{1/2} \\ &=& \frac{1}{2} \\ \end{eqnarray} $$ Now we solve for every other $c_k$. $$ \begin{eqnarray} c_k &=& \frac{1}{2} \int_{-1/2}^{3/2} x(t) e^{- j k \pi t} \; dt \\ &=& \frac{1}{2} \int_{-1/2}^{1/2} e^{- j k \pi t} \; dt \\ &=& \frac{1}{2} \left. \frac{1}{j k \pi} e^{- j k \pi t} \right|_{-1/2}^{1/2} \\ &=& \frac{1}{-j k (\pi/2)} e^{-j k (\pi/2)} - \frac{1}{-j k (\pi/2)} e^{j k (\pi/2)} \\ &=& \left( \frac{1}{-j k (\pi/2)} e^{-j k (\pi/2)} \right) + \left( \frac{1}{-j k (\pi/2)} e^{-j k (\pi/2)} \right)^* \\ &=& \textrm{real} \left\{ \frac{1}{-j k (\pi/2)} e^{-j k (\pi/2)} \right\} \\ &=& \left\{ \begin{array}{l l} \frac{2}{k \pi} &\;,\;& \textrm{if} \; k = \ldots, -15, -11, -7, -3, 1, 5, 9, 13, \ldots \\ \frac{-2}{k \pi} &\;,\;& \textrm{if} \; k = \ldots, -13, -9, -5, -1, 3, 7, 11, 15, \ldots \\ 0 &\;,\;& \textrm{if} \; k \textrm{ is even} \quad \textrm{and} \quad k \neq 0 \\ \end{array} \right. \\ \end{eqnarray} $$ Therefore the final result is $$ \begin{eqnarray} c_k &=& \left\{ \begin{array}{l l} \frac{2}{k \pi} &\;,\;& \textrm{if} \; k = \ldots, -15, -11, -7, -3, 1, 5, 9, 13, \ldots \\ \frac{-2}{k \pi} &\;,\;& \textrm{if} \; k = \ldots, -13, -9, -5, -1, 3, 7, 11, 15, \ldots \\ 0 &\;,\;& \textrm{if} \; k \textrm{ is even} \quad \textrm{and} \quad k \neq 0 \\ 1/2 &\;,\;& \textrm{if} \; k = 0 \end{array} \right. \\ \end{eqnarray} $$