Class 3 (Special Signals)
Periodic signals
The fundamental period
For a continuous-time signal, the fundamental period is the smallest $T_0$ value such that $$x(t) = x(t+m T_0)$$ for any integer value $m$.
For a discrete-time signal, the fundamental period is the smallest $N_0$ value such that $$x[n] = x[n+m N_0]$$ for any integer value of $m$.
The fundamental frequency
The reciprocal of the fundamental $$ f_0 = 1/T_0 \quad \textrm{or} \quad f_0 = 1/N_0 $$ is known as the fundamental frequency of the signal.
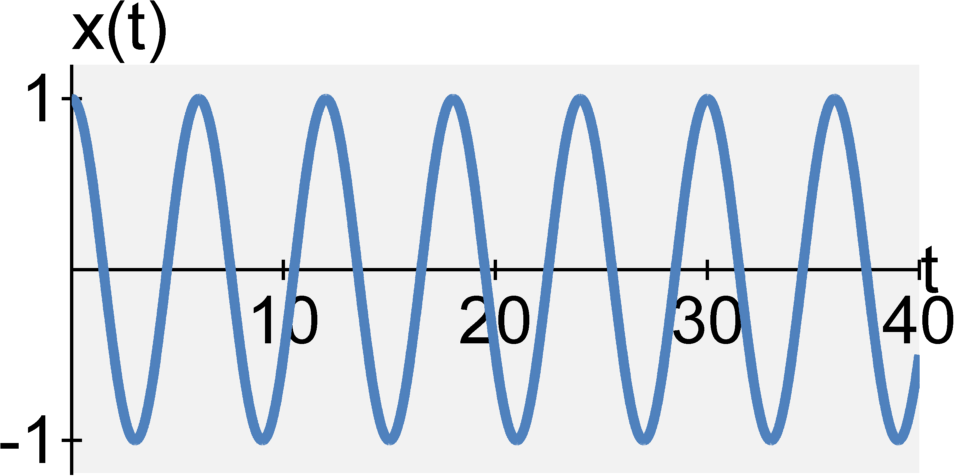
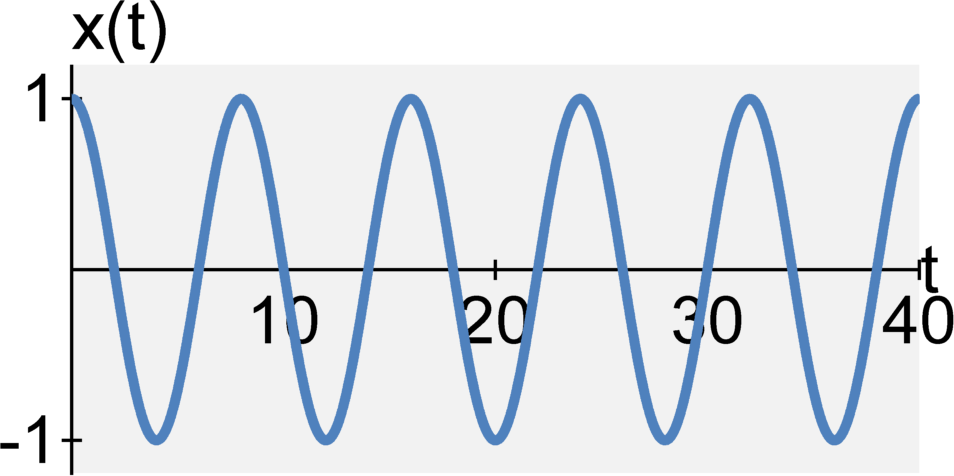
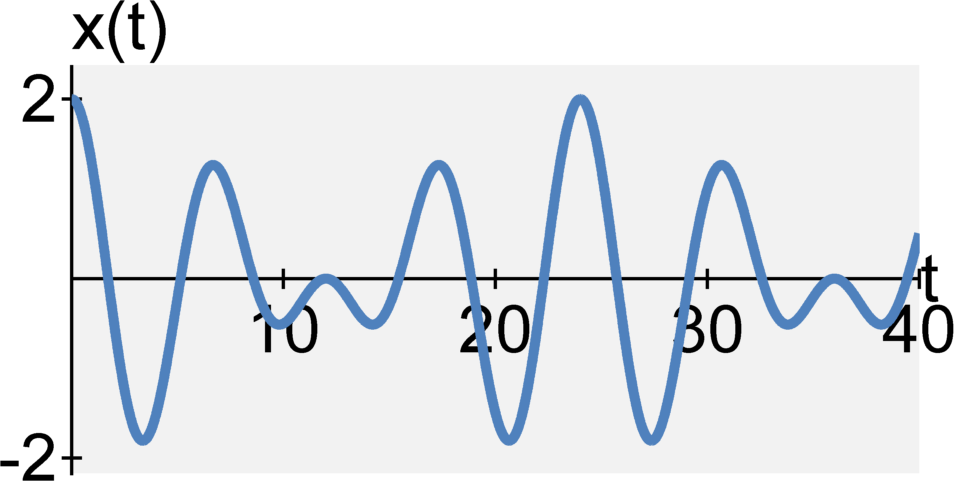
(least common multiple of 6 and 8)
Sums of periodic signals
For a single periodic signal, the fundamental period is the smallest period in that signal. For example, the fundamental period of $$x(t) = \cos(2 \pi t)$$ is $T_0 = 1$.
For a sum of periodic signals $$x(t) = x_1(t) + x_2(t) + x_3(t) + \ldots,$$ the fundamental period is a little more complicated. Assume $T_1, T_2, T_3, \ldots$ are the fundamental periods for Assume $x_1(t), x_2(t), x_3(t), \ldots$. The fundamental period is the first smallest interval $T_0$ in which every signal repeats.
Computing the fundamental period of a sum
From periods
The fundamental period $T_0$ of $x_1(t)+x_2(t)+x_3(t)+\ldots$ is the least common multiple of the individual periods $T_1, T_2, T_3, \ldots$.
From frequencies
The fundamental frequency $F_0$ of $x_1(t)+x_2(t)+x_3(t)+\ldots$ is the greatest common divisor of the individual frequencies $f_1, f_2, f_3, \ldots$. The fundamental period is then the reciprocal of the fundamental frequency.
Special functions / signals
Impulse functions
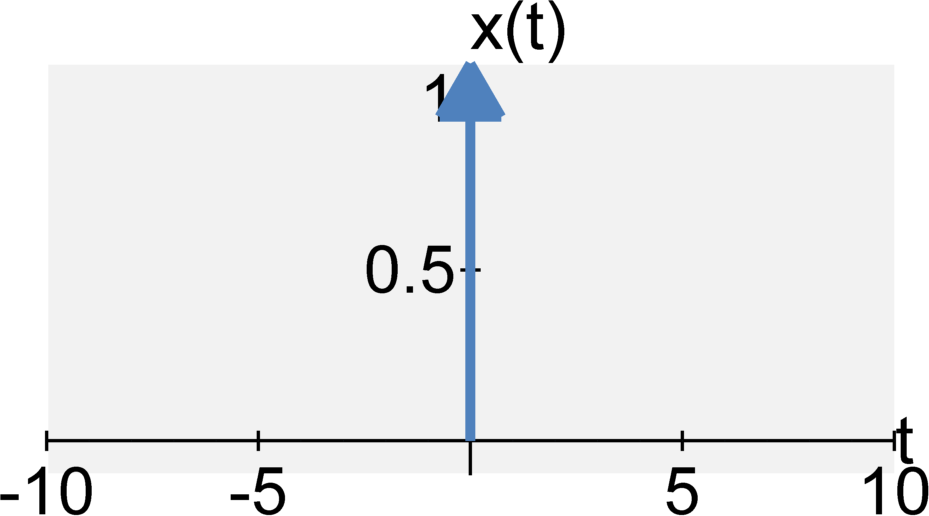
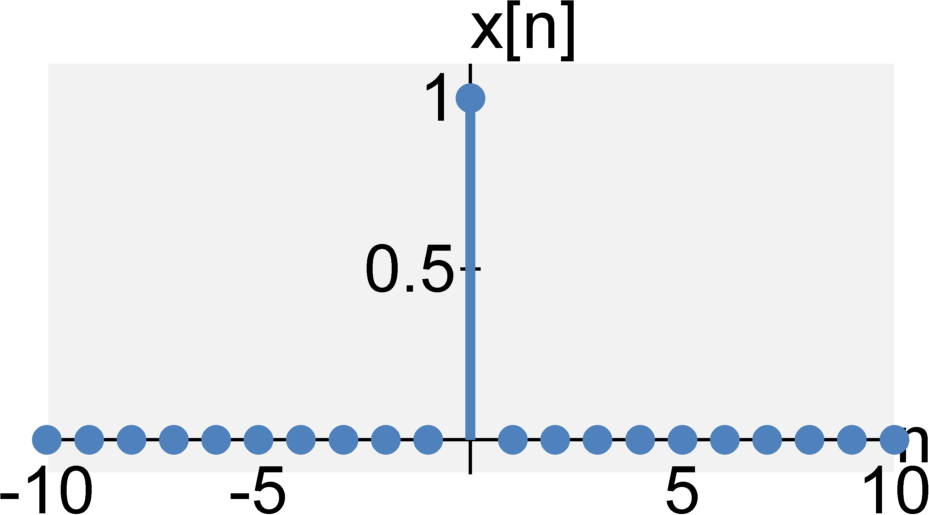
The Dirac $\delta$ signal (continuous-time impulse signal) is defined by $$ \delta(t) = \left\{ \begin{eqnarray} \infty &\quad& \textrm{for} \quad t = 0 \\ 0 &\quad& \textrm{for} \quad t \neq 0 \end{eqnarray} \right. $$ where $$\int_{-\infty}^{\infty} \delta(t) dt = 1 $$
The Kronecker $\delta$ signal (discrete-time impulse signal) is defined by $$ \delta[n] = \left\{ \begin{eqnarray} 1 &\quad& \textrm{for} \quad n = 0 \\ 0 &\quad& \textrm{for} \quad n \neq 0 \end{eqnarray} \right. $$
The properties of impulse signals:
- Energy: $E_{x} = \textrm{Not well defined}$
- Power: $P_{x} = 0$
- Even / Odd?: Even (Understanding why is beyond the purview of this course. You will not be tested on this.)
- Periodic?: No
- Causal?: Yes
Heaviside step functions
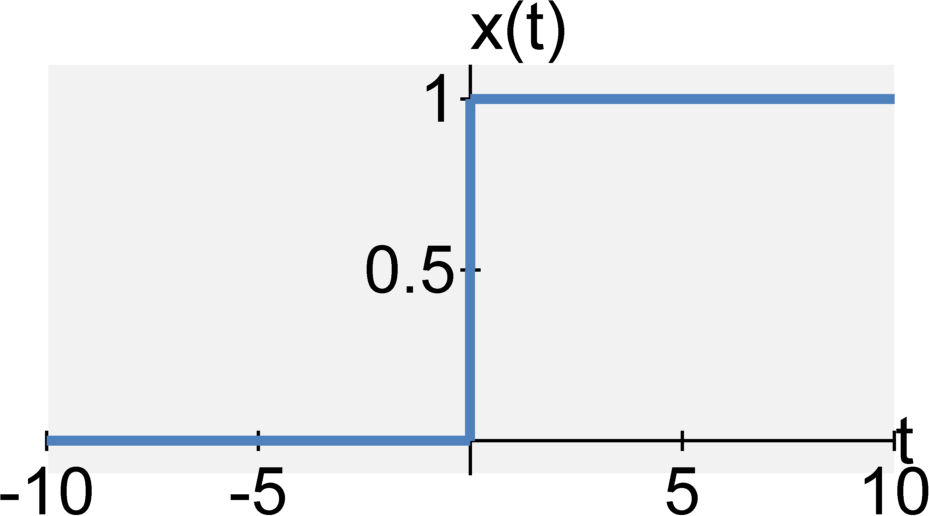
The continuous-time step function $u(t)$ is defined by $$ u(t) = \int_{-\infty}^{t} \delta(\tau) d\tau = \left\{ \begin{eqnarray} 1 &\quad& \textrm{for} \quad t \geq 0 \\ 0 &\quad& \textrm{for} \quad t < 0 \end{eqnarray} \right. $$
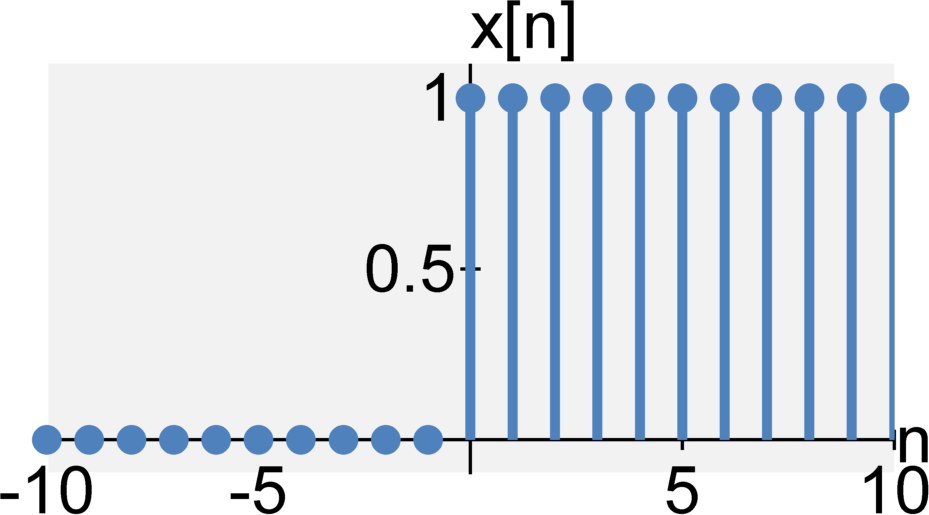
The discrete-time step function $u[n]$ is defined by $$ u[n] = \sum_{k = -\infty}^{n} \delta[k] = \left\{ \begin{eqnarray} 1 &\quad& \textrm{for} \quad n \geq 0 \\ 0 &\quad& \textrm{for} \quad n < 0 \end{eqnarray} \right. $$
The properties of the Heaviside step functions:
- Energy: $E_{x} = \infty$
- Power: $P_{x} = 1/2$
- Even / Odd?: Neither
- Periodic?: No
- Causal?: Yes
Other Important Signals
Cosines and sines
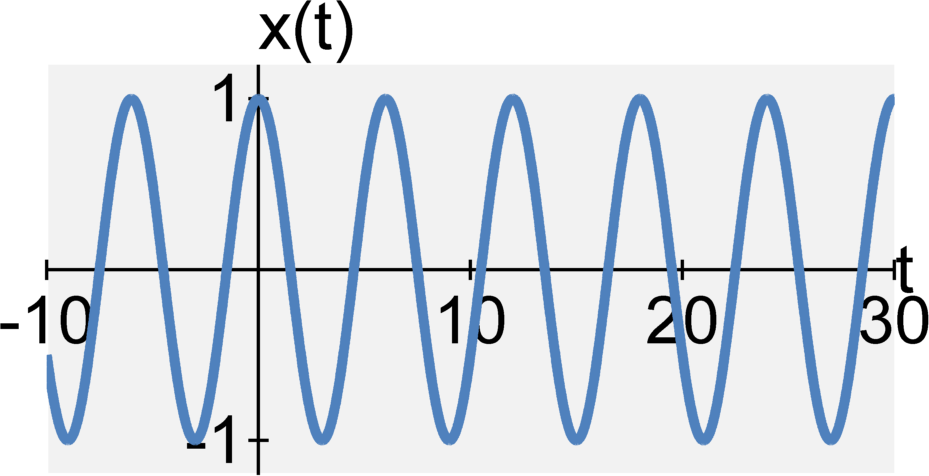
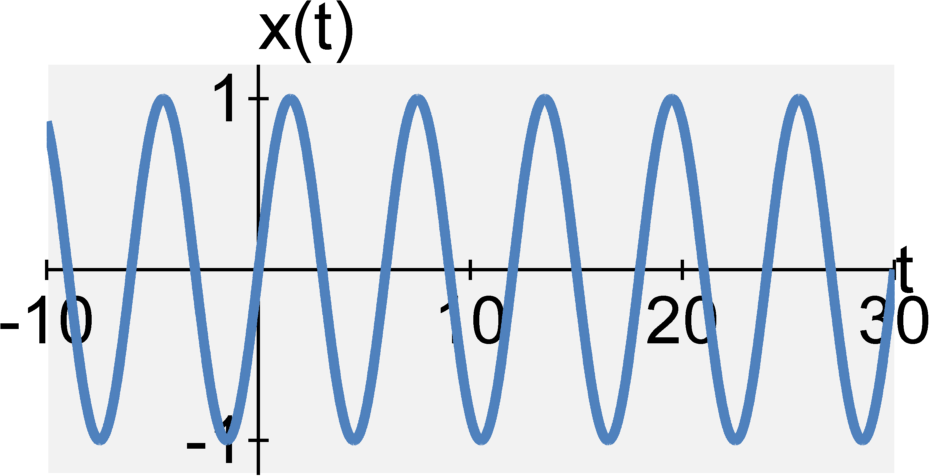
The continuous-time cosine and sine signals are defined by $$ x_1(t) = \cos(\omega_0 t) \quad , \quad x_2(t) = \sin(\omega_0 t) $$
The properties of the continuous-time cosines or sines:
- Enegry: $E_{x} = \infty$
- Power: $P_{x} = 1/2$
- Even / Odd?: $\cos(\omega_0 t)$ is even and $\sin(\omega_0 t)$ is odd
- Periodic?: Yes
- Fundamental frequency: $f_0 = \omega_0/(2 \pi)$
- Fundamental period: $T_0 = 1/f_0$
- Causal?: No
Stepped exponential
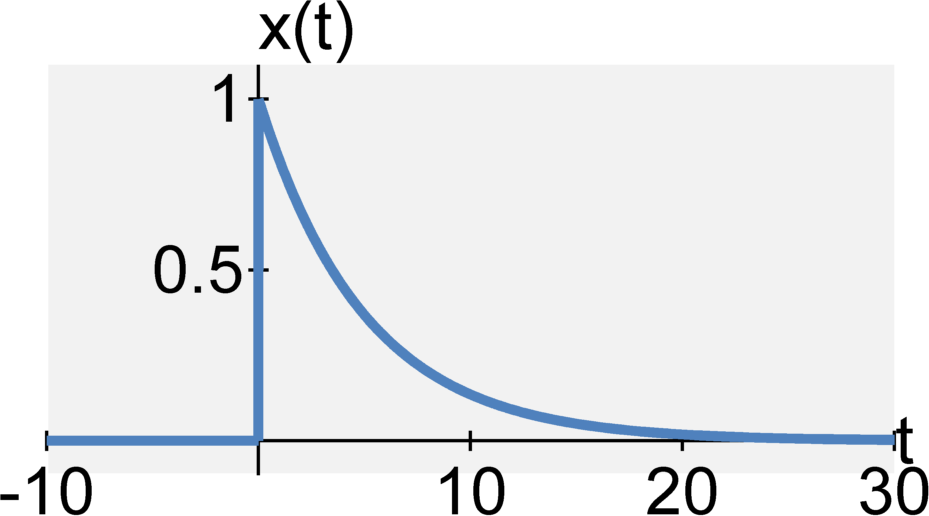
A continuous-time exponential signal is defined by $$ x(t) = e^{a_0 t} u(t) $$
The properties of the exponential signals are:
- Enegry: $E_{x} = \left\{ \begin{eqnarray} \infty &\quad& \textrm{for} \quad a_0 \geq 0 \\ - 1/(2 a_0) &\quad& \textrm{for} \quad a_0 < 0 \end{eqnarray} \right.$
- Power: $P_{x} = 0$
- Even / Odd?: No
- Periodic?: No
- Causal?: Yes
Complex exponentials
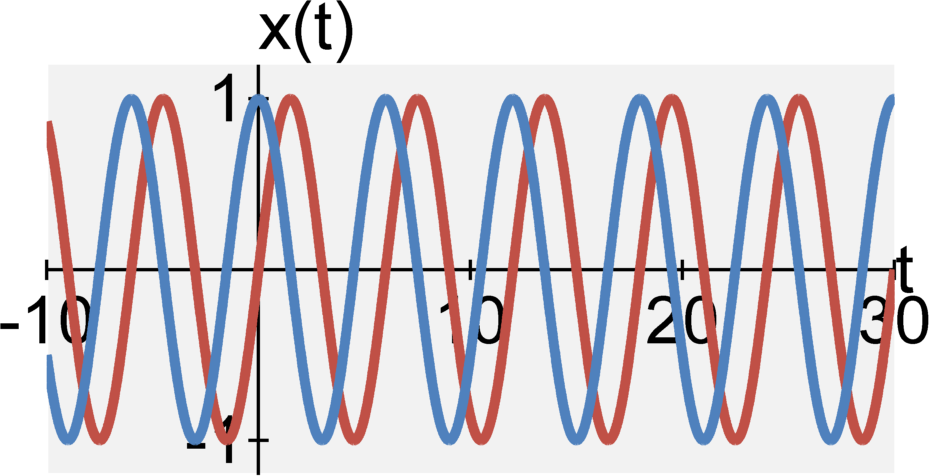
The continuous-time complex exponential signal is defined by $$ \begin{eqnarray} x(t) &=& e^{(j \omega_0 + a_0)t} \\ &=& \cos(\omega_0 t) + j \sin(\omega_0 t) \end{eqnarray}$$
The properties of the continuous-time complex exponential:
- Enegry: $E_{x} = \infty$
- Power: $P_{x} = 1$
- Even / Odd?: No, but its components are: $\cos(\omega_0 t)$ is even and $\sin(\omega_0 t)$ is odd
- Periodic?: Yes
- Fundamental frequency: $f_0 = \omega_0/(2 \pi)$
- Fundamental period: $T_0 = 1/f_0$
- Causal?: No
Stepped general exponential
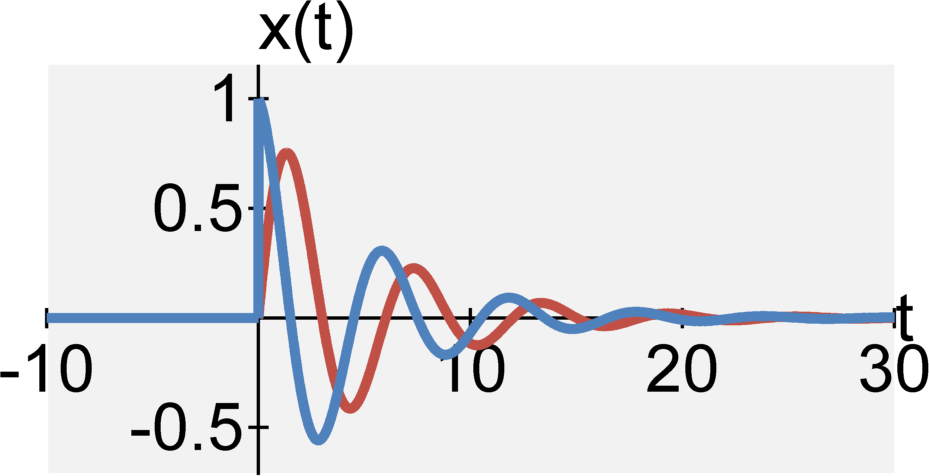
The continuous-time general exponential signal is defined by $$ \begin{eqnarray} x(t) &=& e^{(j \omega_0 + a_0)t} u(t) \\ &=& \left[ e^{a_0 t} \cos(\omega_0 t) + j e^{a_0 t} \sin(\omega_0 t) \right] u(t) \end{eqnarray}$$
The properties of the general exponential signals are:
- Enegry: $E_{x} = \left\{ \begin{eqnarray} \infty &\quad& \textrm{for} \quad a_0 \geq 0 \\ - 1/(2 a_0) &\quad& \textrm{for} \quad a_0 < 0 \end{eqnarray} \right.$
- Power: $P_{x} = 0$
- Even / Odd?: No
- Periodic?: No
- Causal?: Yes
Additional Resources
- From this course
- From Richard Baraniuk's open textbook
- Common Discrete Time Signals
- Continuous Time Complex Exponential
- Discrete Time Complex Exponential