April 10, 2012 - Been Awhile

It has been awhile since I've had time to update this page. I have been working very hard on a filter bank multicarrier spread spectrum transceiver design using LabVIEW, VHDL, and LabVIEW FPGA. More on that later, I hope. The fdesign.py file that I have posted down there will work but I have newer better versions that I will post. My focus has shifted away from MIMO Detection to filter bank multicarrier. I have recently submitted a journal paper and a conference paper. More on that later.

As part of my training, I have completed two courses sponsored by Xilinx on VHDL. I am trying to learn how to layout a board for FPGA design, but progress has been slow as I have so many other things going on. I am still thinking about MIMO Detection in my spare time (particularly ways to improve MCMC). I believe I have found one, but I am searching for time to pursue it. I have been playing racquetball and tennis whenever I get a chance. I am so excited to be able to enjoy the summer sunshine!

I am taking a class from Dr. Mathews called Advanced Digital Signal Processing II. We have studied Prinicpal Component Analysis (including some nonlinear signal processing problems) with applications in classification and parameter estimation. In addition, we have spent a large part of the semester pursuing a better understanding of Independent Component Analysis which has been an exciting journey (albeit a confusing one). My final project involves using ICA as a preprocessing step to improve user detection in multiple access scenarios where multiple access interference (MAI) may be present. I'll probably post the code and final paper here when it is complete.

November 22, 2010 - Snow, snow, snow, and filtering...

Well, it finally snowed a bunch. It had to come (actually it came much later this year). I'm hoping to go snow shoeing sometime this year. I need to get out or else I'll go crazy! :)

Anyway, I have several more developments. I have created a filter design script in Python. This script is capable of designing "optimal" low-pass FIR filters. They are optimal in the least squares sense. I used Quasi Monte Carlo integration in it so I suppose that makes it slightly less optimal, but if you compare the results to the optimal ones (where the integration is performed analytically), there is virtually no difference in the frequency response. I have decided to post my script up here in the hopes that it may be useful to anyone else out there doing DSP with Python. I would love to hear from you if it works. Also, if you have suggestions or questions, please send them my way. You can email me at wasden (at) eng (.dot) utah (.dot) edu. The script requires numpy and matplotlib (it only requires matplotlib if you want to see plots of the frequency response, otherwise just numpy). In this post, you'll find an example 31 tap filter that was designed with the script.

Filter Frequency Response

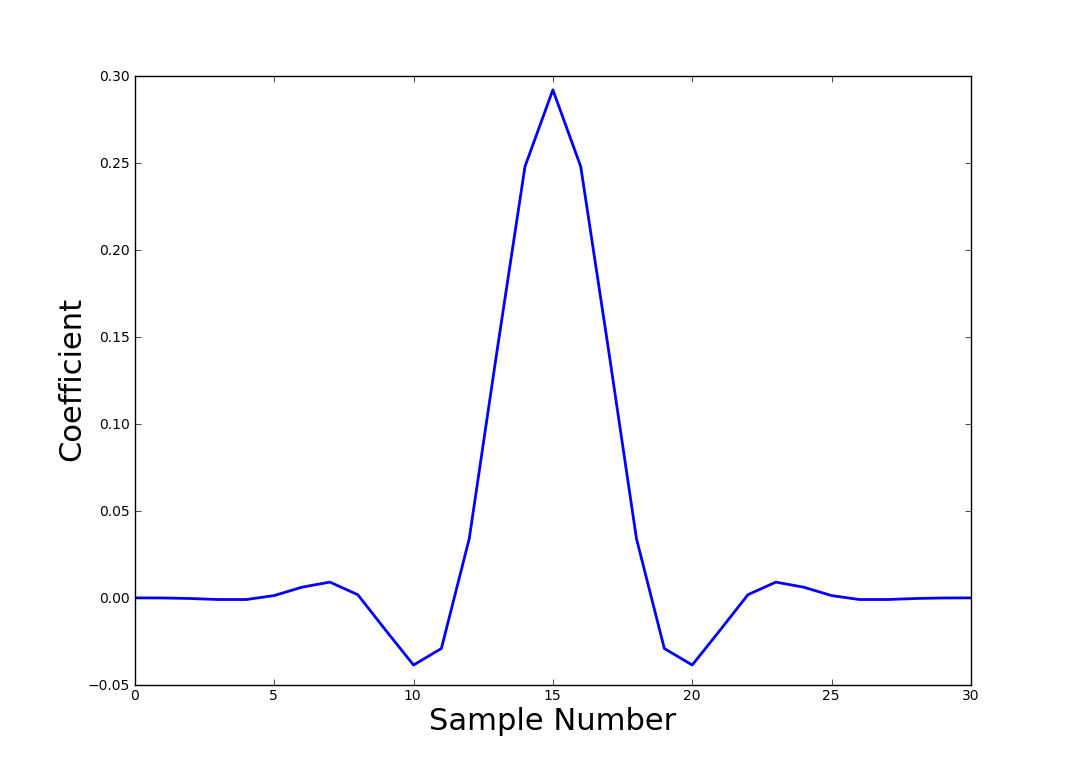
Filter Impulse Response

The script can be found here. I will probably update it and create a better version as time moves on so that I can use it for all my filter design needs.

In addition, I did a very simple QMF simulation. It has the perfect reconstruction property using the simple two-tap fir filters [0.5,0.5] and [0.5,-0.5]. Again, any questions, comments, or criticisms are welcome.

November 17, 2010 - Kalman Filter

I am implementing a Kalman Filtering package in Python in order to compare the tracking abilities of the Particle Filter with another possibility. I will also compare it to the LMS and RLS algorithms. Though, I suspect that the Kalman Filter and Particle Filter will perform better than both of those since they are based on Wiener filters which assume the input is a stationary process (and therefore needs no tracking).

I am including a quick plot below demonstrating the performance of the Kalman filter. This is the projection of the first tap of a four tap filter. The underlying process is a Gauss-Markov process with perfectly known statistics for this simulation example.

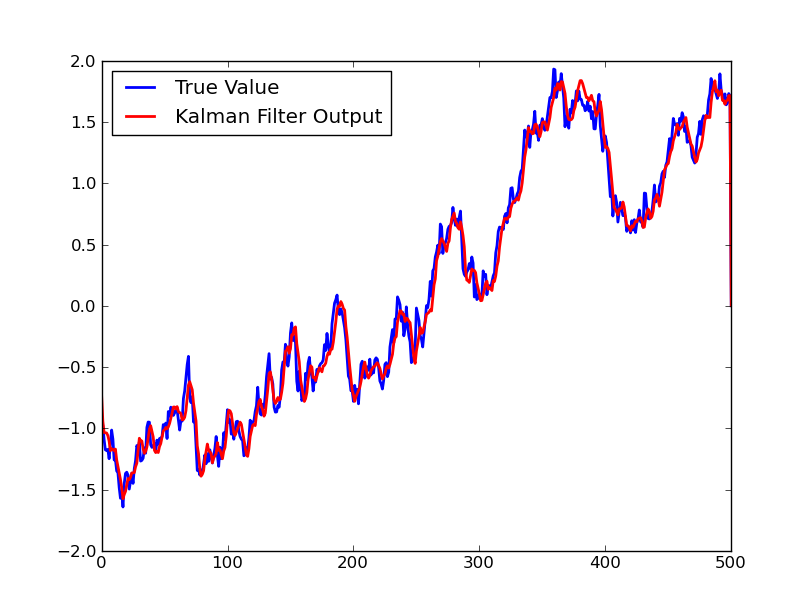
Kalman Filter (Projection to first axis)

Kalman Filter Learning Curve

Above we have a plot of the first tap being tracked and, below that, a typical learning curve for my Kalman Filter implementation so far. This learning curve shows that the filter converges very quickly, but has a higher error in its output than that of the Particle Filter. I am hoping to present a comparison of these methods and a combination of them in my class project for my Adaptive Filters class.

Implementation details and equations for the Kalman filter used for the channel equalization problem are given here.

November 15, 2010 - Particle Filtering Update

I have been hard at work on using particle filtering as an alternative tool (as opposed to the LMS algorithm, RLS algorithm, Kalman Filtering, etc) for filter modeling problems. I am hoping to someday apply this to the MCMC Detector to create a robust way of tracking the channel.

To demonstrate some of the work that I have been doing, here are two plots. The bottom one is a plot of a sequential importance sampling (SIS) filter. The top one is a plot of a sequential importance resampling (SIR) filter applied to the same problem.

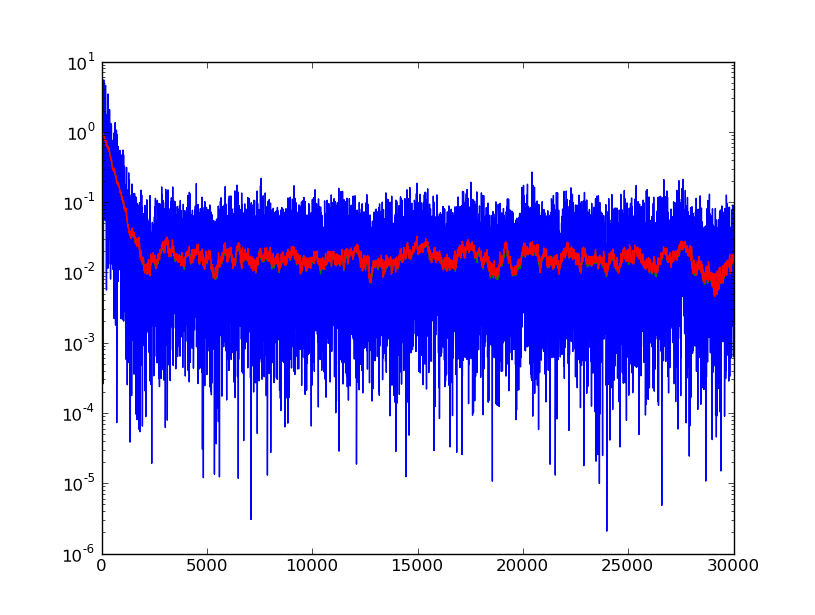
SIR Particle Filter

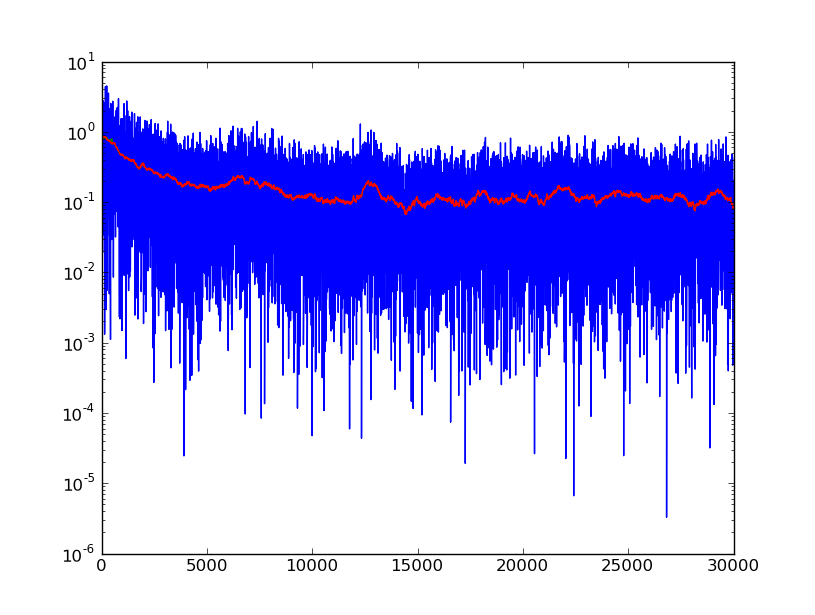
SIS Particle Filter

The blue represents the error in the filter output and the received output samples. The additive noise is 0.1 so that is why the error level is so high. The red is calculated by multiplying the difference of each filter tap in the estimated filter with the true filter tap by its complex conjugate and then summing these quantities. It is therefore a measure of the total squared error in the estimate and the filter. There are a total of 32 taps in the filter for this simulation. The filter that is being tracked is a time-varying filter that was calculated through a Gauss=Markov process. Only ten particles were used in both simulations.

I find it interesting that the resampling has some very important and intuitive consequences. First, the SIR filter converges faster. Secondly, it has a lower error after convergence. Thirdly, and most importantly in the case of the time-varying channel is its ability to adapt quickly to sudden changes. You can kind of see this above in that the error in its estimates are less smooth than the error output by the SIS particle filter.

November 9, 2010 - Python and Particle Filtering

Well, I am now working on a particle filter for channel estimation/tracking. I have a working implementation in Python. I have also given some time over to developing a Python implementation for adaptive filtering. Specifically, it includes the LMS (and several variants) for modeling and inverse modeling. I will add the RLS algorithms to it and then post the package here. I am hoping to compare the results of the adaptive filtering algorithms with the particle filter. I am also working on my qualifying exam this semester, so time is tight.

I have thoroughly enjoyed converting most of my numerical work over to Python. It has been fun. There are no Python packages that I am aware of for implementing fading channels. To this end, I am converting my C code which produces a Rayleigh channel through a sum of sinusoids technique (Jakes model and a generalized Jakes model) to Python. I will use SWIG to create an interface between Python and my C code. Both of these provide a fair approximation to Clarke's Model. A filtered white noise model will also be included. More information on Rayleigh fading can be found here.

A preliminary version of the python package can be downloaded here. If you read the readme.txt file, then you will find brief instructions on how to use it for your own simulations. More information regarding the process used for the simulation is given in the following paper: Improved Models for the Generation of Multiple Uncorrelated Rayleigh Fading Waveforms by Yahong R. Zheng and Chengshan Xiao. It was published in IEEE Communications Letters 2002. Note: The current package only works on linux-based systems.