Tool:      For n independent samples, Xi, from a normal (or gaussian) distribution with mean μ and variance σ2, the probability density function of the normalized sample variance,

(where ν = n − 1, 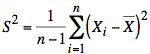, and )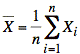

has a chi‑squared distribution with ν degrees of freedom:

or

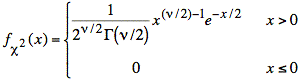
Proof:    As in most analyses of sample variance, we split into two pieces by adding and subtracting the true mean, μ:

This gives us independent random variables in each term and allows us to rewrite the summation for c 2 as follows:

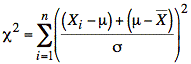
or

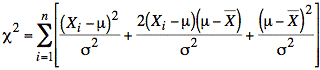
or

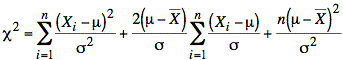
or

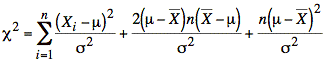
or

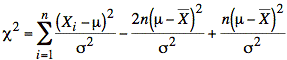
or

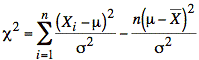
The second term is the square of a normal (or gaussian) random variable that we will refer to as Z:

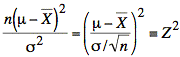
For , we have the following mean and variance:

   and     

When we subtract μ and scale by to get Z we have a standard normal (or gaussian) random variable with a mean of zero and a variance of 1.

    and     

Thus, Z is chi-squared distributed with one degree of freedom.

Returning to the first term of χ2, we observe that it is the sum of squared normal (or gaussian) random variables that we will refer to as Zi:

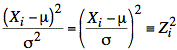
Since we are subtracting the mean and dividing by the standard deviation of the Xi, the Zi have standard normal (or gaussian) distributions. Consequently, the are all chi-squared distributed. Thus, is a sum of chi-squared random variables and is a chi-squared random variable with n degrees of freedom.

χ2 is, in turn, the difference of chi-squared distributed random variables. We write this symbolically as follows:

or

But this means that χ2 must be equivalent to a chi-squared distributed random variable with n − 1 degrees of freedom:

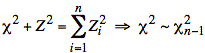
Ref:        Ronald E. Walpole, Raymond H. Myers, Sharon L. Myers, and Keying Ye, Probability and Statistics for Engineers and Scientists, 8th Ed., Upper Saddle River, NJ: Prentice Hall, 2007.