Ex:            A probability density function, f(X), is shown below. Use the center of mass method to find E(X), the expected value of X.

Sol'n:       When parts of f(X) are horizontally symmetrical, we can replace them with a point mass located at their center of mass. The value of the point mass is the area of that portion of f(X).

Mathematically, the point mass is represented by a delta (or impulse) function:

where m ≡ mass and c ≡ location of center of mass

For the f(X) given in this problem, the half circle has an area of 1/4 and is centered at −1/2. The "M" has an area of 1/4 + 1/4 = 1/2 centered at 1, and the rectangle has an area of 1/4 centered at 5/2.

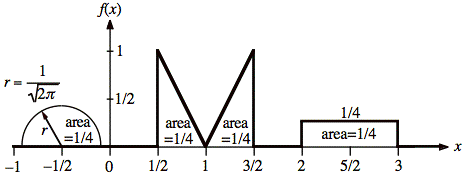
These areas are equivalent to point masses as shown below:

Mathematically, the new f(x) is a summation of delta functions:

Computing the expected value of this new f(x) we have the following formal steps, (the first few steps of which may be bypassed, as explained below):

We apply the following identity several times:

This yields the following expression that is the sum of center points times centers of mass, (an expression which may be written down directly without going through the preceding steps):

Note:       The center-of-mass method may be applied to any shapes, but it is simplest in the case where shapes are horizontally symmetric.