By: Neil E. Cotter	Probability
		Combinatorics
		5-card game

---

Game: Card deck is 4 suits, cards 1 to 5 in each suit.

Deal two sets of three cards: first set is one card up and two cards down, while second set is two cards up and one card down.

Team calculates probability of outcomes (see next page) and chooses which hand they think will be best.

Turn the down cards up and see which set of cards is better according to the odds chart in Table I, below. (Table I lists hands from best at top to worst at bottom.)

If team chooses correctly, they get 1 point, otherwise 0 points.

Winning team has highest percentage of correct guesses. At least five rounds must be played. Tied hands are possible: guessing either hand scores 1 point.

Number of possible hands:

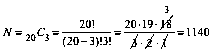
Table I

Odds of Getting Hands (before dealt)

(from best hand to worst hand)

Hand	# of such hands	Explanation
3 of same # (3-of-a-kind)		5 #'s, use 3 of the 4 of that #
3 of same suit (flush)		4 suits, 3 of 5 cards in suit used
3 in a row (straight)		3 ways to get 3-in-row: 123, 234, 345; 4 suit choices each card, minus 3-in-a-row (same suit) * 4 suits
2 of same # (pair)		5 #'s for pair, use 2 of 4 of that #, 16 cards for 3rd card (and not get 3 of kind)
2 of same suit (small flush)		4 suits, use 2 of 5 cards of that suit, 15 cards for 3rd (and not get 3 flush) *includes some 2 of kind and some 3 in a row
2 in a row (small straight)		ways to get 2-in-row: 124, 125, 134, 145, 235; 4 suits for each card **includes some flush and small flush