Class 22 (The Discrete-Time Fourier Transform)

The Discrete-Time Fourier Transform (DTFT)

Discrete-time Fourier transform analysis, i.e., the [forward] Discrete-time Fourier transform , is defined by $$X(\Omega) = \sum_{n = -\infty}^{\infty} x[n] e^{-j \Omega n } $$

Continuous-time Fourier transform synthesis, i.e., the inverse Discrete-time Fourier transform , is defined by $$x[n] = \frac{1}{2 \pi} \int_{2 \pi} X(\Omega) e^{j \Omega n } d \Omega$$

Derivation

Recall, a sampled signal is defined by $$\begin{eqnarray*} x_s(t) &=& \sum_{n=-\infty}^{\infty} x(t) \delta(t - n T_s) \\ &=& \sum_{n=-\infty}^{\infty} x(n T_s) \delta(t - n T_s) \; . \end{eqnarray*}$$ where $T_s$ is the sampling period of the sampled signal. Therefore, the Fourier transform of $x_s(t)$ is defined as $$\begin{eqnarray*} X(\omega) &=& \int_{-\infty}^{\infty} x_s(t) e^{-j \omega t} \; dt \\ &=& \int_{-\infty}^{\infty} \sum_{n=-\infty}^{\infty} x(n T_s) \delta(t - n T_s) e^{-j \omega t} \; dt \\ &=& \sum_{n=-\infty}^{\infty} x(n T_s) \int_{-\infty}^{\infty} \delta(t - n T_s) e^{-j \omega t} \; dt \\ &=& \sum_{n=-\infty}^{\infty} x(n T_s) e^{-j \omega n T_s} \; . \end{eqnarray*}$$ Now let us define $\Omega = \omega T_s$ and the discrete-time signal $x[n] = x(n T_s)$. With these substitutions, we get $$\begin{eqnarray*} X(\omega) &=& \sum_{n=-\infty}^{\infty} x[n] e^{-j \Omega n} \; . \end{eqnarray*}$$ This is the known as the Discrete-time Fourier Transform.

Frequency domain periodicity

Consider the values of $X(\Omega)$ and $X(\Omega + 2 \pi)$. This is defined by $$\begin{eqnarray*} X(\Omega + 2 \pi) &=& \sum_{n = -\infty}^{\infty} x[n] e^{-j (\Omega + 2 \pi) n } \\ &=& \sum_{n = -\infty}^{\infty} x[n] e^{-j \Omega n + j 2 \pi n} \\ &=& \sum_{n = -\infty}^{\infty} x[n] e^{-j \Omega n } e^{j 2 \pi n} \\ &=& \sum_{n = -\infty}^{\infty} x[n] e^{-j \Omega n } (1) \\ &=& \sum_{n = -\infty}^{\infty} x[n] e^{-j \Omega n } \; . \end{eqnarray*}$$ Since $n$ is an integer, we know that $e^{j 2 \pi n} = \cos(2 \pi n) + j \sin(2 \pi n) = 1$. Therefore, $$\begin{eqnarray*} X(\Omega + 2 \pi) &=& \sum_{n = -\infty}^{\infty} x[n] e^{-j \Omega n } (1) \\ &=& \sum_{n = -\infty}^{\infty} x[n] e^{-j \Omega n } \; . \end{eqnarray*}$$

Hence, the spectrum generated by the discrete-time Fourier transform is periodic with period $2 \pi$. Note that we get the same effect if we sample a continuous-time signal with a sampling period $T_s = 1$ (i.e., $f_s = 1$ and $\omega_s = 2 \pi$).

Typically, we look at frequency in one period from $-\pi to \pi$, where $0$ is the lowest frequency (before periodicity) and $-\pi$ and $\pi$ are the highest negative and positive freqencies. This gives us the concepts to develop high pass and low pass filters.

A shifted impulse

Question 0(a): Compute the Discrete-time Fourier Transform of $$x[n] = \delta[n - 2] \; .$$

Solution: The Discrete-time Fourier Transform of the impulse is $$ \begin{eqnarray*} X(\Omega) &=& \sum_{n = -\infty}^{\infty} \delta[n - 2] e^{-j \Omega n } \\ &=& \sum_{n = -\infty}^{\infty} \delta[n - 2] e^{-j \Omega (2) } \\ &=& e^{-j \Omega (2) } \\ \end{eqnarray*} $$

Geometric progression

Question 1(a): Compute the Discrete-time Fourier Transform of $$x[n] = (1/2)^{n} u[n] \; .$$

Solution: The Discrete-time Fourier Transform of this geometric sequence is $$\begin{eqnarray*} X(\Omega) &=& \sum_{n = -\infty}^{\infty} (1/2)^{n} u[n] e^{-j \Omega n } \\ &=& \sum_{n = 0}^{\infty} (1/2)^{n} e^{-j \Omega n } \\ &=& \sum_{n = 0}^{\infty} ((1/2) e^{-j \Omega})^{n} \\ \end{eqnarray*}$$ From this, we can use the geometric series identity for a summation, which states $$\sum_{k=0}^{\infty} a r^k = a \left( \frac{1}{1-r} \right) \; .$$ Applying this identity gives us $$\begin{eqnarray*} X(\Omega) &=& \frac{1}{1-(1/2)e^{-j \Omega}} \\ \end{eqnarray*}$$

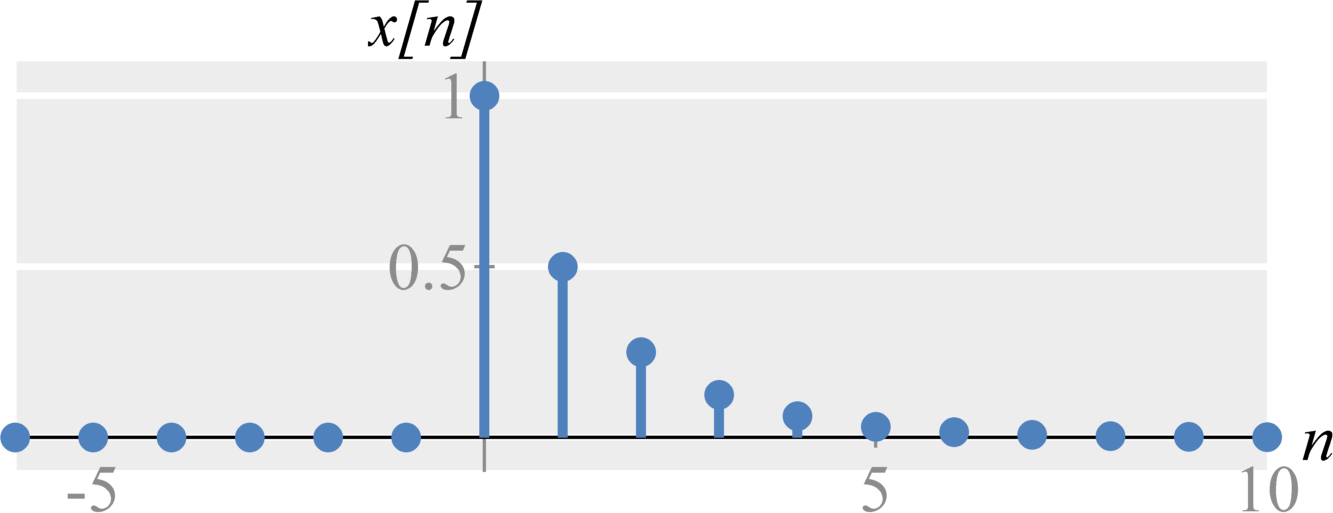
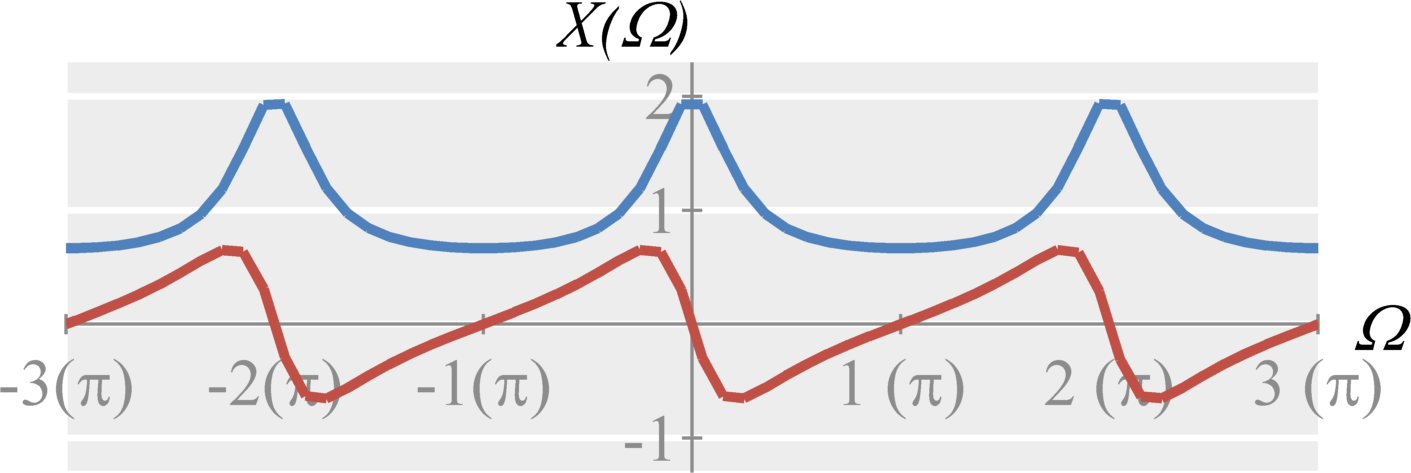
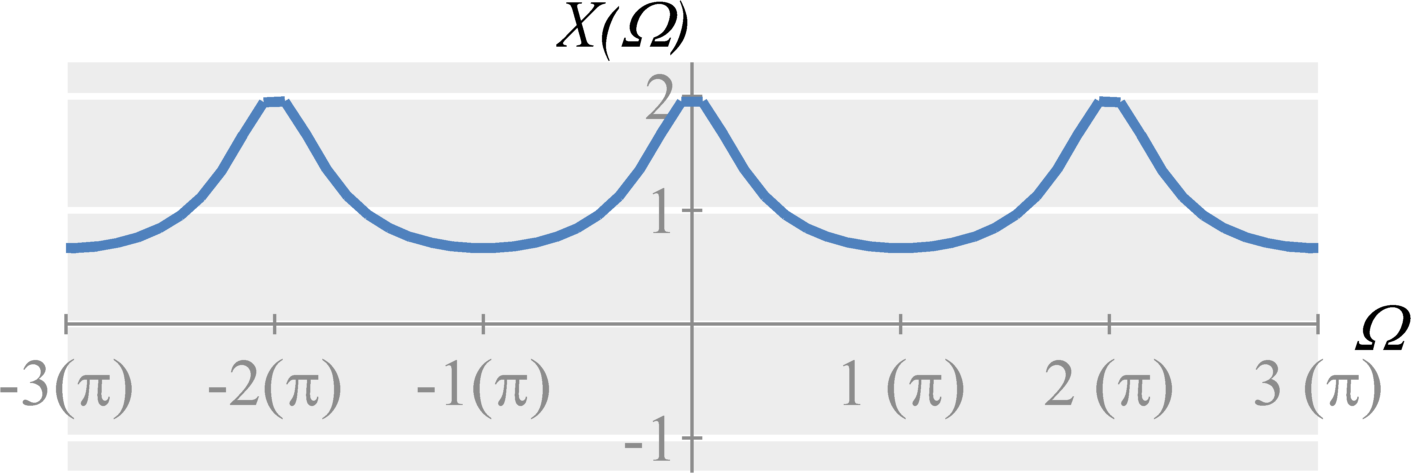
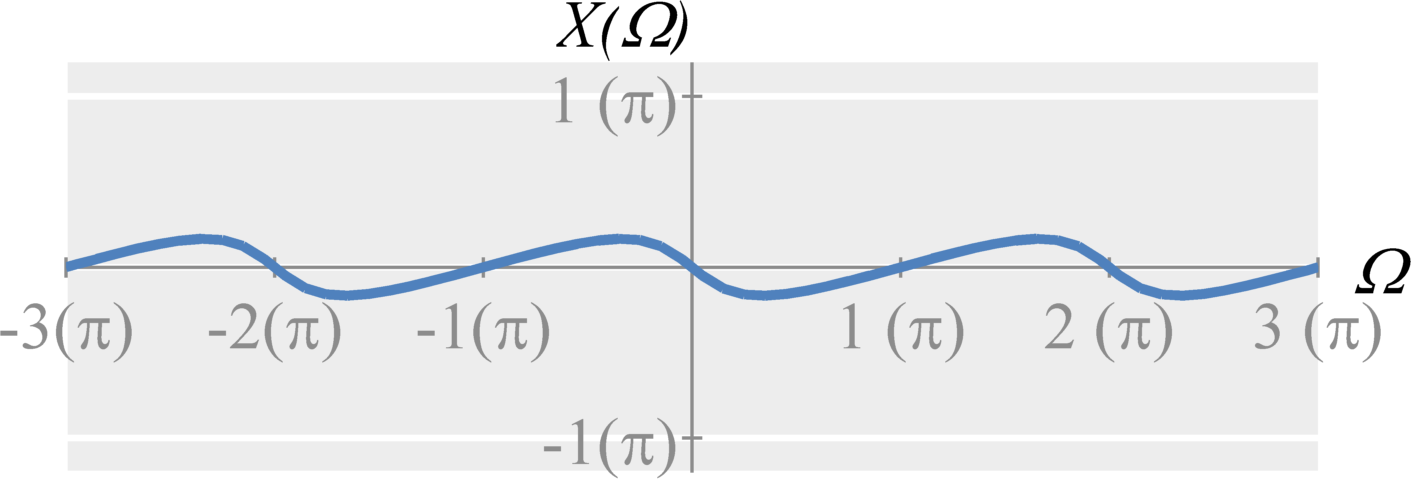
Question 1(b): Compute the magnitude of $X(\Omega)$ (the above result)

Solution: The magnitude can be expressed by $$\begin{eqnarray*} |X(\Omega)| &=& \frac{1}{|1-(1/2)e^{-j \Omega}|} \\ &=& \frac{1}{|1-(1/2) \cos(\Omega) + j (1/2) \sin(\Omega)|} \\ &=& \frac{1}{\sqrt{(1 - (1/2) \cos(\Omega))^2 + ((1/2) \sin(\Omega))^2}} \\ &=& \frac{1}{\sqrt{1-\cos(\Omega) + (1/4)\cos^2(\Omega) + (1/4) \sin^2(\Omega)}} \\ &=& \frac{1}{\sqrt{1-\cos(\Omega) + (1/4)}} \\ &=& \frac{1}{\sqrt{(5/4) - \cos(\Omega)}} \end{eqnarray*}$$ When $\Omega = 0$, then $|X(0)| = 1/(\sqrt{1/4}) = 2$. When $\Omega = \pi$, then $|X(\pi)| = 1/(\sqrt{9/4})=2/3$. Therefore the result is similar to a lowpass filter.

A moving average system

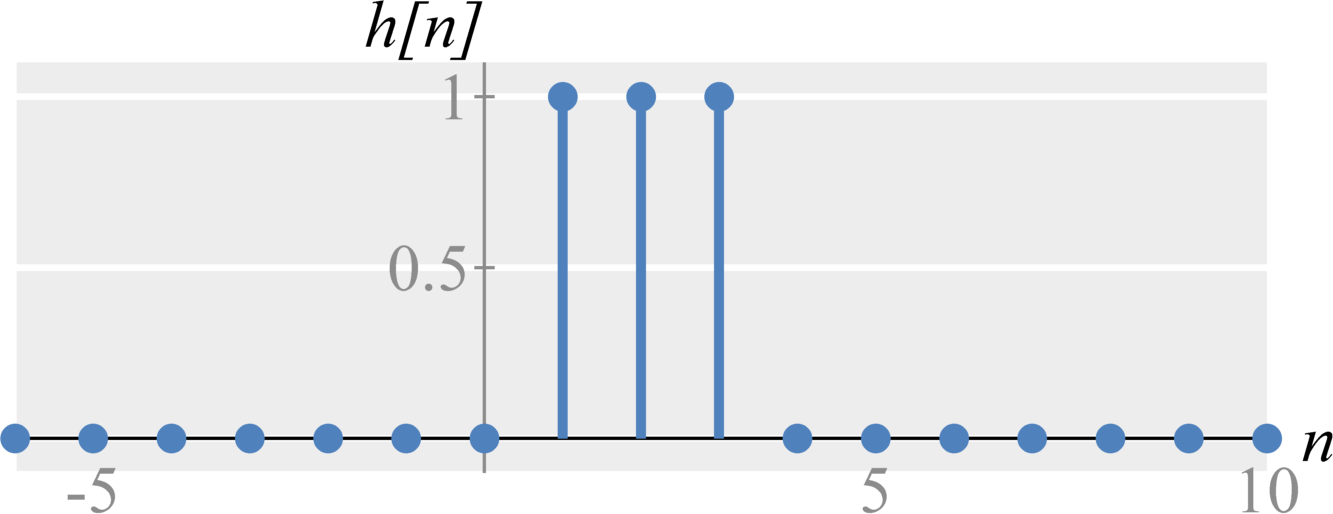
Question 2(a): Compute $H(\Omega)$, the Discrete-time Fourier Transform of the delayed moving average system $$h[n] = \frac{1}{3} \left( \delta[n-1] + \delta[n-2] + \delta[n-3] \right) \; .$$

Solution: The Discrete-time Fourier Transform of this sequence is $$\begin{eqnarray*} H(\Omega) &=& \sum_{n = -\infty}^{\infty} \frac{1}{3} \left( \delta[n-1] + \delta[n-2] + \delta[n-3] \right) e^{-j \Omega n } \\ &=& \frac{1}{3} \left( e^{-j \Omega } + e^{-j 2 \Omega } + e^{-j 3 \Omega } \right) &=& \frac{1}{3} e^{-2 j \Omega } \left( e^{+ j \Omega } + 1 + e^{-j \Omega } \right) \end{eqnarray*}$$

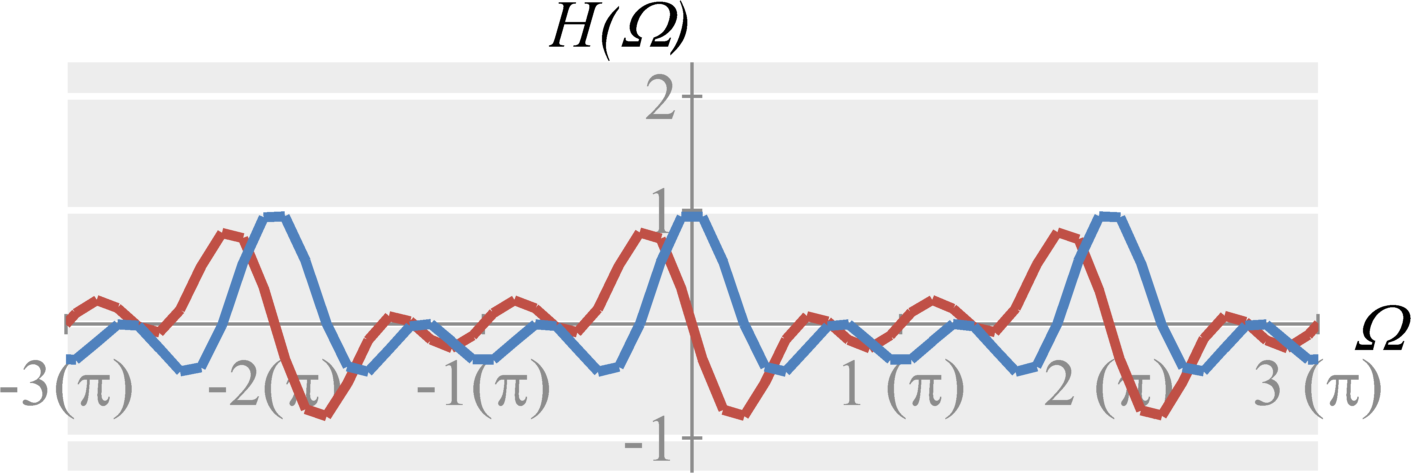
Question 2(b): Compute the magnitude of $H(\Omega)$.

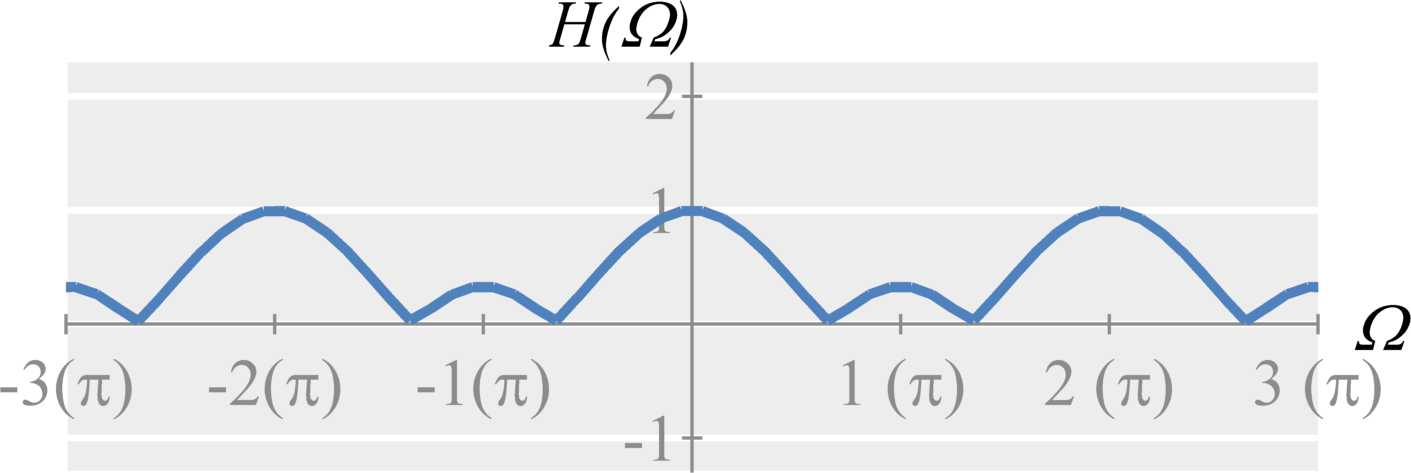
Solution: We can rewrite $H(\Omega)$ as $$\begin{eqnarray*} H(\Omega) &=& \frac{1}{3} e^{-2 j \Omega } \left( e^{+ j \Omega } + 1 + e^{-j \Omega } \right) \\ &=& \frac{1}{3} e^{-2 j \Omega } \left( e^{+ j \Omega } + 1 + e^{-j \Omega } \right) \\ &=& \frac{1}{3} \left( 1 + 2 \cos(\Omega) \right) e^{-2 j \Omega } \; . \end{eqnarray*}$$ Therefore, the magnitude is $$\begin{eqnarray*} |H(\Omega)| &=& \frac{1}{3} \left| 1 + 2 \cos(\Omega) \right| \end{eqnarray*}$$

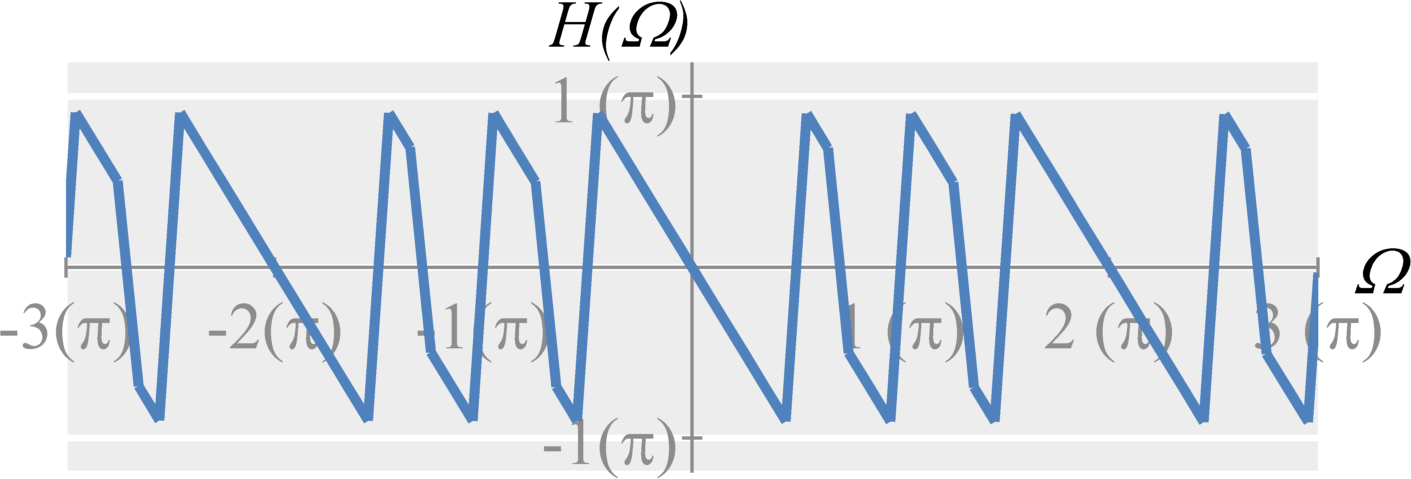
Question 2(c): Compute the phase of $H(\Omega)$.

Solution: In the previous solution, we wrote $H(\omega)$ as $$\begin{eqnarray*} H(\Omega) &=& \frac{1}{3} e^{-2 j \Omega } \left( 1 + 2 \cos(\Omega) \right) \; . \end{eqnarray*}$$ From this, we can see that the phase for $-\pi$ to $\pi$ (and repeated every $2\pi$) is defined by $$\begin{eqnarray*} \angle H(\Omega) &=& - 2 \Omega + \tan^{-1} \left( \frac{1}{ 1 + 2 \cos(\Omega)} \right) \end{eqnarray*}$$ Note that the second term is necessary because $1+ 2\cos(\Omega)$ is real but not strictly positive (i.e., the negatives create a $\pm pi$ change in phase).

A general box

Question 3(a): Compute $H(\Omega)$, the Discrete-time Fourier Transform of a box from $-N$ to $N$ $$h[n] = \sum_{m=-N}^{N} \delta(n-m) \; .$$

Solution: The DTFT of an impulse $\delta(n-m)$ is $e^{-j\Omega m}$. Therefore, $$ \begin{eqnarray*} H(\Omega) &=& \sum_{m=-N}^{N} e^{-j\Omega m} \\ &=& \sum_{m=-N}^{N} \left( e^{-j\Omega} \right)^m \end{eqnarray*} $$ The generalized geometric series equation states that $$ \begin{eqnarray*} \sum_{k=a}^{b} r^k = \frac{r^a - r^{b+1}}{1 - r} \; . \end{eqnarray*} $$ Applying this gives us $$ \begin{eqnarray*} H(\Omega) &=& \frac{e^{j\Omega N} - e^{-j\Omega (N+1)}}{1 - e^{-j\Omega}} \\ &=& \frac{e^{-j\Omega (1/2)} \left[e^{j\Omega (N + 1/2)} - e^{-j\Omega (N+1/2)} \right]}{ e^{-j\Omega (1/2)} \left[ e^{j\Omega (1/2)} - e^{-j\Omega (1/2)} \right]} \\ &=& \frac{\sin(\Omega [N + 1/2])}{\sin(\Omega / 2)} \end{eqnarray*} $$