Class 14 (Amplitude Modulation [Communications])
Introduction
Most electromagnetic antennas are "tuned" to operate at around one-half or one-quarter of the frequency of transmitted data. Raw vocal or instrumental music has a frequencies up to around $300$ Hz. Given a speed of light $c$, the wavelength of an electromagentic carrying this information would be approximately $1000$ km long. Therefore, our antennas would need to be about $250$ km to $500$ km, or $2300$ to $4600$ American football fields, long to transmit this information.
Amplitude modulation addresses this challenge by shifting low-frequency content to high frequencies. After the high-frequency is received at an antenna, amplitude demodulation is used to shift the high-frequency content back to the original lower frequency.
Double-Sideband Amplitude Modulation
Amplitude modulation is based on the multiplication property of the Fourier transform, $$ x(t) y(t) \stackrel{\mathcal{F}}{\longleftrightarrow} \frac{1}{2 \pi} X(\omega) * Y(\omega) \; .$$ Specifically, if we choose $y(t) = \cos(\omega_c t)$, we get $$ x(t) \cos(\omega_c t) \stackrel{\mathcal{F}}{\longleftrightarrow} \frac{1}{2 \pi} X(\omega) * \left[ \pi(\delta(\omega - \omega_c) + \delta(\omega + \omega_c)) \right] $$ Convolution with an impulse is the same as shifting. Therefore, $$X(\omega) * \delta(\omega - \omega_c) = X(\omega - \omega_c)$$ $$X(\omega) * \delta(\omega + \omega_c) = X(\omega + \omega_c) \; .$$
Therefore, double-sideband amplitude modulation with a cosine carrier is expressed as $$ x(t) \cos(\omega_c t) \stackrel{\mathcal{F}}{\longleftrightarrow} \frac{1}{2} \left( X(\omega-\omega_c) + X(\omega+\omega_c) \right) \;. $$ Similarly, double-sideband amplitude modulation with a sine carrier is expressed as $$ x(t) \sin(\omega_c t) \stackrel{\mathcal{F}}{\longleftrightarrow} \frac{1}{2 j} \left( X(\omega-\omega_c) - X(\omega+\omega_c) \right) \;. $$ The frequency $\omega_c$ is known as the carrier frequency. The signal $\cos(\omega_c t)$ or $\sin(\omega_c t)$ is known as the carrier signal.
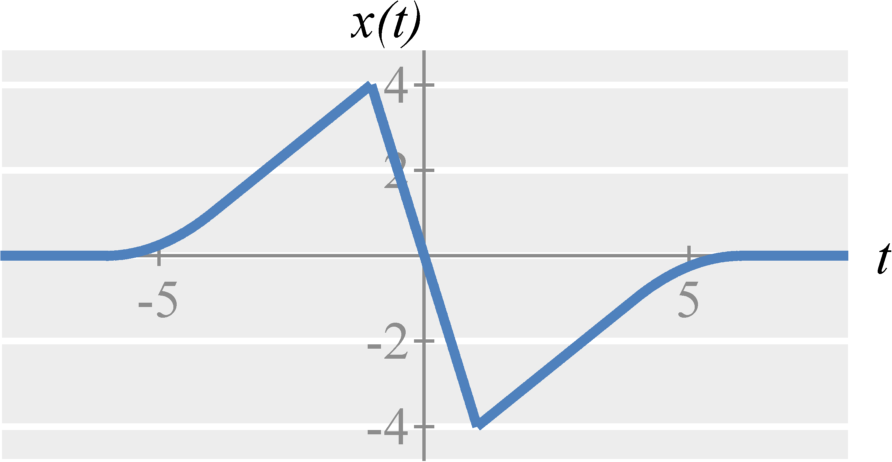
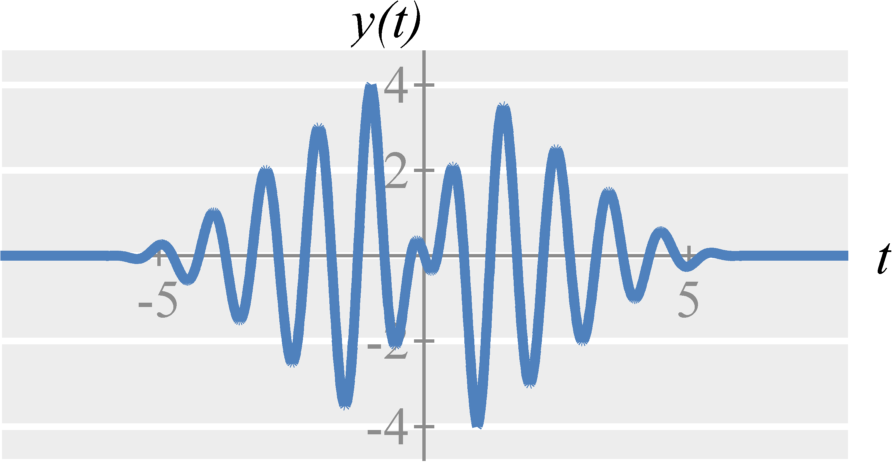
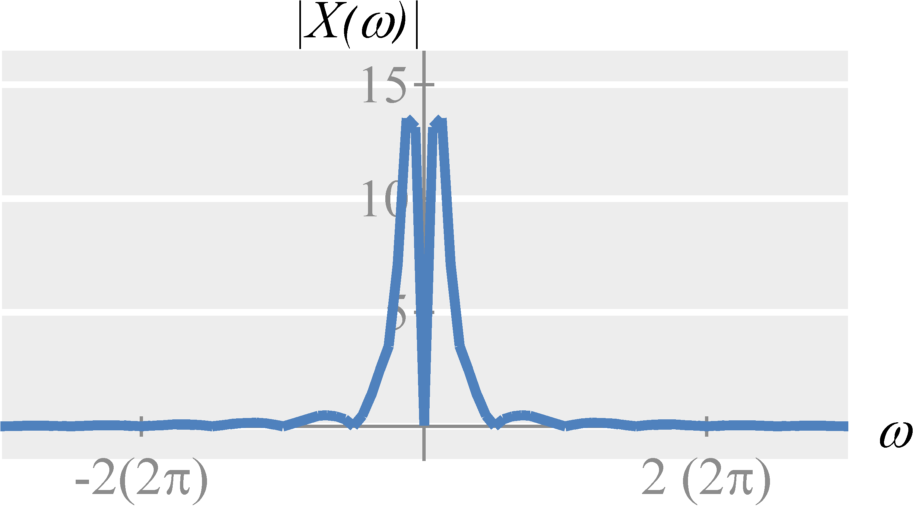
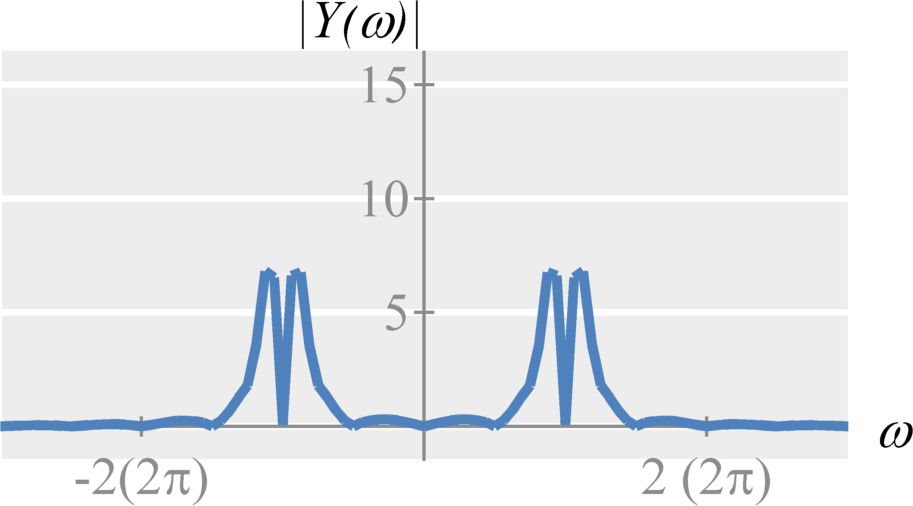
Double-Sideband Amplitude Demodulation
After a signal is recieved, we demodulate it to get back the original signal. Demodulating signal is a two-step process: multiplication and low-pass filtering.
Step one -- Modulation Again: We again multiply the signal with the carrier signal. According to the multiplication property, we get $$ \left[ x(t) \cos(\omega_c t) \right] \cos(\omega_c t) \stackrel{\mathcal{F}}{\longleftrightarrow} \frac{1}{2 \pi} \left[ \frac{1}{2} \left( X(\omega-\omega_c) + X(\omega+\omega_c) \right) \right] * \left[ \pi(\delta(\omega - \omega_c) + \delta(\omega - \omega_c)) \right] \; .$$ When we simplify this expression, we get $$ \left[ x(t) \cos(\omega_c t) \right] \cos(\omega_c t) \stackrel{\mathcal{F}}{\longleftrightarrow} \frac{1}{4} \left( X(\omega-2\omega_c) + 2 X(\omega) + X(\omega+2\omega_c) \right) \; . $$ Of these three terms, we have two high-frequency signals $X(\omega-2\omega_c)$ and $X(\omega+2\omega_c$) and the original, low-frequency signal, $X(\omega)$.
Step two -- Filtering: We now use a low-pass filter to retain only the original signal $X(\omega)$. For simplicity, we assume we can use an ideal low-pass filter with a gain (amplitude) of $2$, $$ H_{low}(\omega) = 2\left[ u(\omega + \omega_c) - u(\omega - \omega_c) \right] \; .$$ When we apply the filter to our result from step 1, we get back only the original signal $$ \frac{1}{4} \left( X(\omega-2\omega_c) + 2 X(\omega) + X(\omega+2\omega_c) \right) H_{low}(\omega) = X(\omega) \; . $$
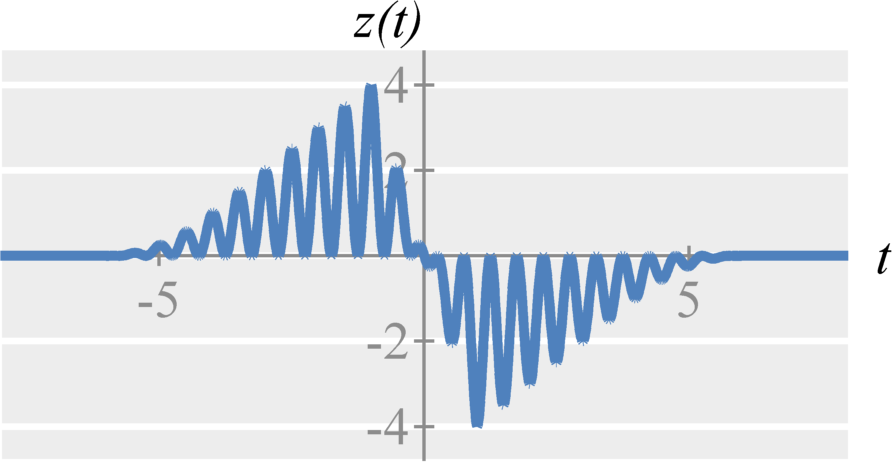
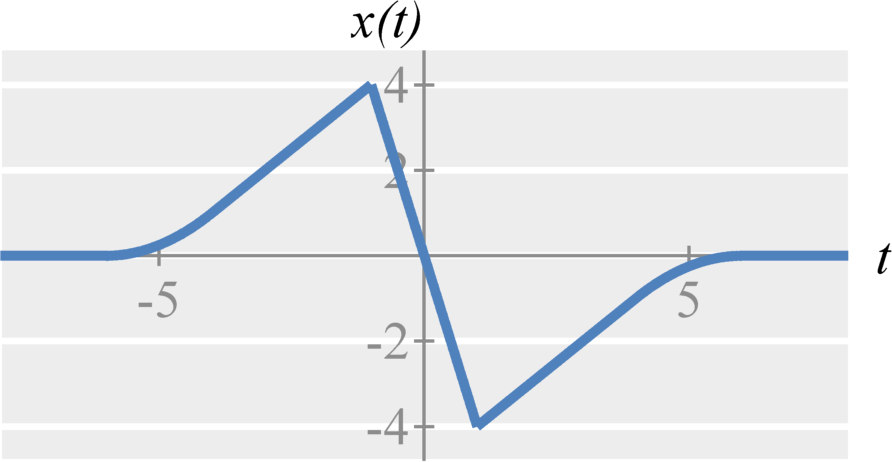
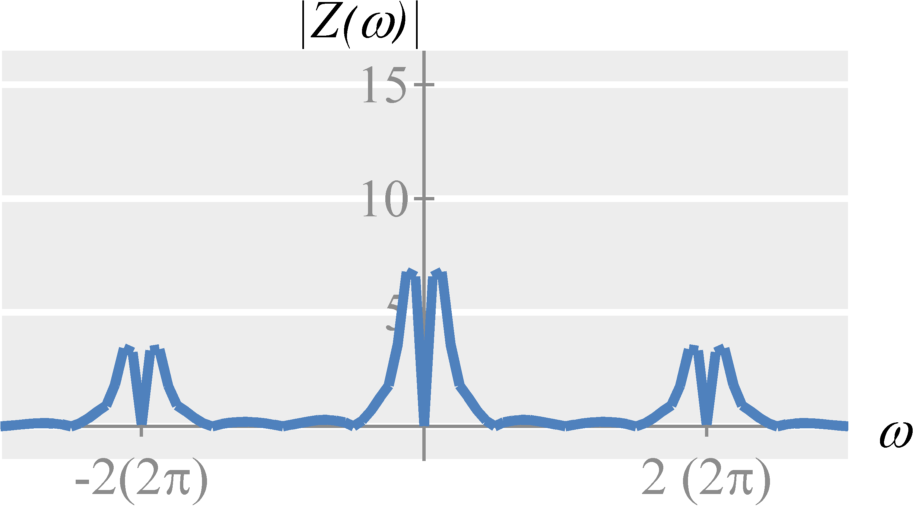
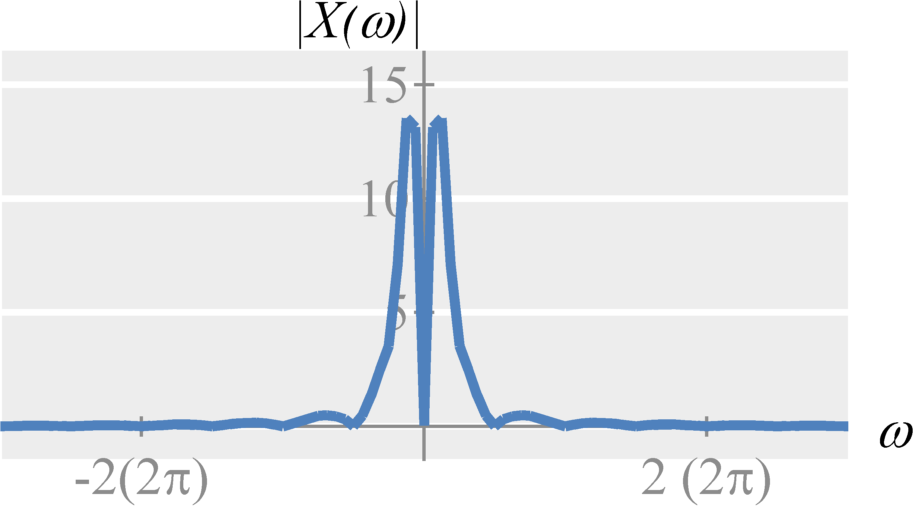
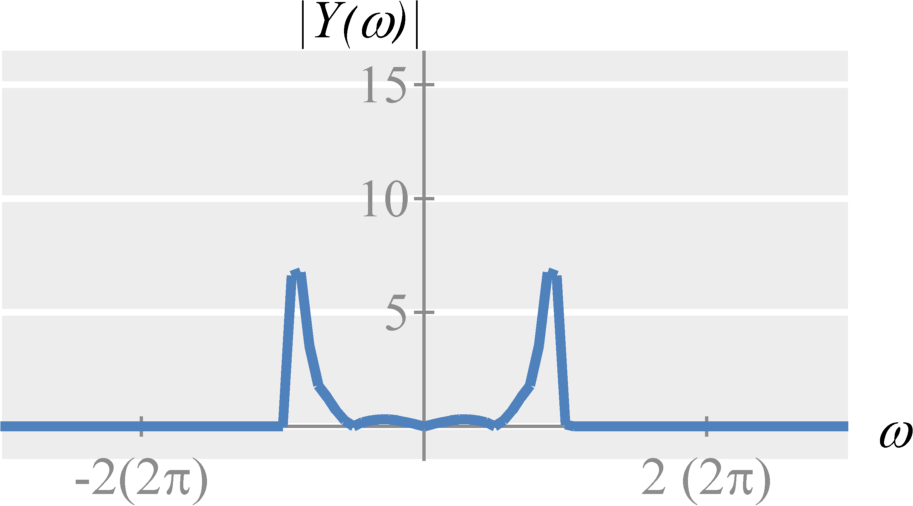
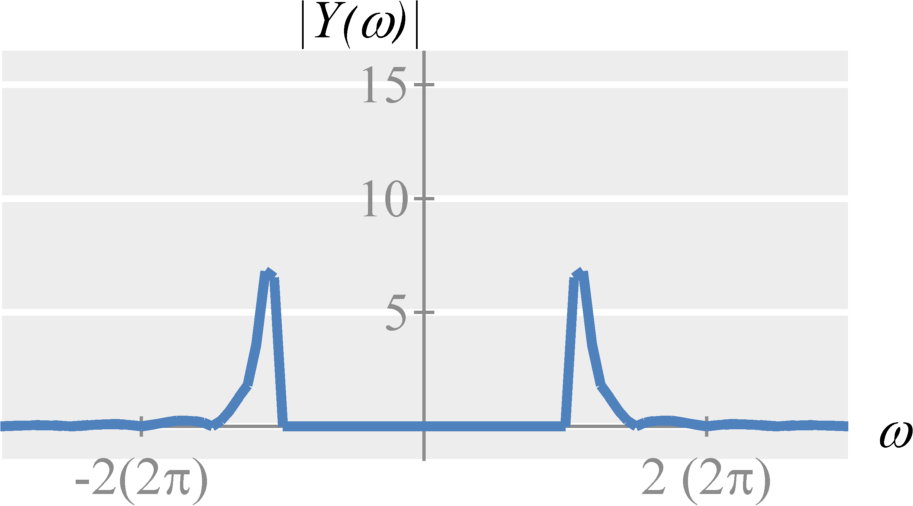
Single-Sideband Amplitude Modulation
Standard amplitude modulation uses more frequency bandwidth than necessary. Both the negative and positive frequencies of the modulated signal contain the same signals. Therefore, we are transmitting redundant information. However, we can remove this redundant information and still be able to reconstruct the original signal. We can do this by applying an ideal low-pass or high-pass filter to the modulated signal before transmission.
Therefore, single-sideband amplitude modulation with a cosine carrier can be expressed in the frequency domain as $$X_{ssb} = \frac{1}{2} \left( X(\omega-\omega_c) + X(\omega+\omega_c) \right) H(\omega) \; .$$ Similarly, single-sideband amplitude modulation with a sine carrier can be expressed in the frequency domain as $$X_{ssb} = \frac{1}{2 j} \left( X(\omega-\omega_c) - X(\omega+\omega_c) \right) H(\omega) \; .$$ The filter can either be an ideal lowpass filter $$H(\omega) = 2 \left[ u(\omega + \omega_c) - u(\omega - \omega_c) \right] \; .$$ Or the filter can be an ideal highpass filter $$H(\omega) = 2 \left[ u(- \omega - \omega_c) +u(\omega - \omega_c) \right] \; .$$ We introduce a gain of two so that the demodulation step remains the same. This is known as single-sideband amplitude modulation.
The single-sideband demodulation is identical to the double-sideband demodulation.
Asyncronous (or noncoherent) Amplitude Modulation
For double-sideband and single-sideband, we need the phase of the received signal to match with the demodulating carrier signal. If the phases do not match, we would achieve imperfect demodulation. We can synchronize the phases, but this requires expensive hardware. To get around this limitation, we use an asynchronous amplitude modulation method.
Modulation
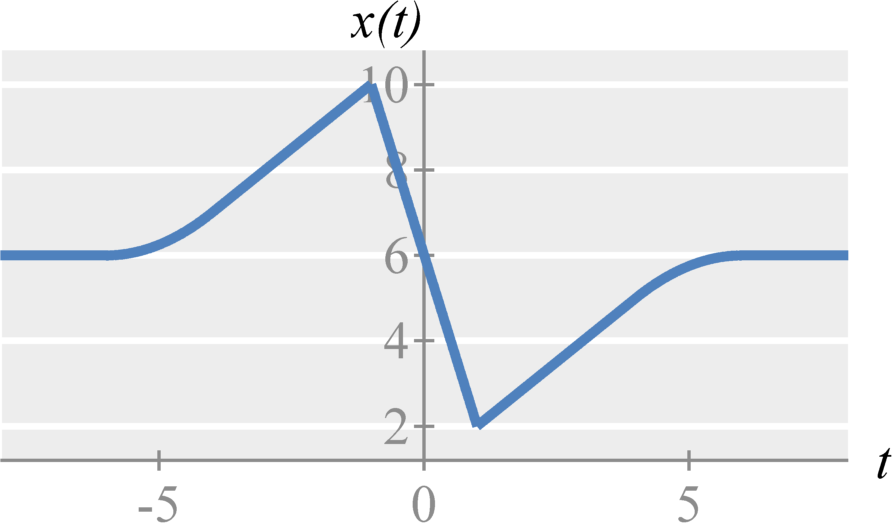
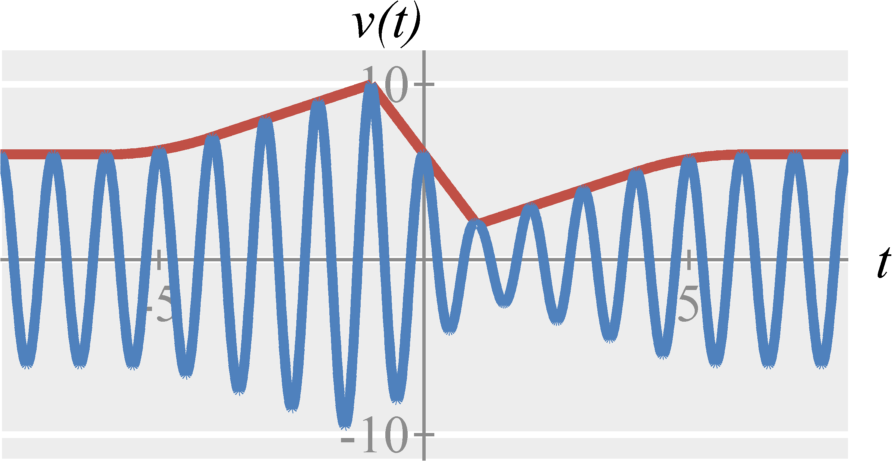
We define asynchronous amplitude modulation (sometimes just referred to as standard amplitude modulation) with a cosine carrier as $$ \left( A + x(t) \right) \cos(\omega_c t) \stackrel{\mathcal{F}}{\longleftrightarrow} \frac{1}{2} \left( X(\omega-\omega_c) + X(\omega+\omega_c) \right) + A \left( \delta(\omega + \omega_c) + \delta(\omega_c - \omega_c t) \right) \;. $$ where $A + x(t) \geq 0$ for all $t$. This ensures that the signal envelope has no zero crossings. Therefore, the $x(t)$ can be extracted directly from the envelope.
Demodulation (The envelope detector)
We can now demodulate the received signal (without knowing its phase) by extracting the envelope. This can be accomplished using a rectifier circuit.
Additional Resources
- From this course
- From Richard Baraniuk's open textbook
- Other online resources