Unit 4                                                       

2270                              PRACTICE EXAM SOLUTION Prob 3                                     

 

3.      (40 points)

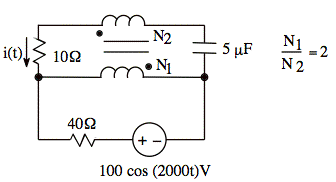
a.   Write a numerical time-domain expression for the current i(t).

 

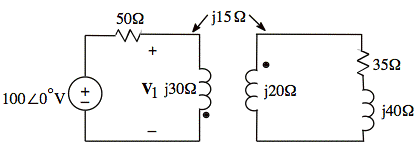
b.   Calculate V1.

 

 

ans:  a)

         b)

 

 

sol'n:  (a)   We assume an ideal transformer since we are only given the turns ratio N1/N2. We want to draw the circuit in the s-domain with labels for I1, I2, V1, and V2.

Our circuit diagram in the s-domain:

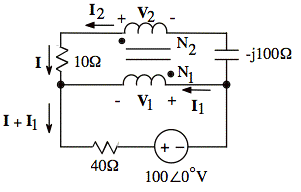
Note:   We measure V1 and V2 with plus signs at dots on transformer.

I1 (primary side) flows into dotted terminal.

I2 (secondary side) flows out of dotted terminal.

For the above definitions of I1, I2, V1, and V2, we have ideal transformer equations without minus signs:

           

Now we write equations for mesh (current) loops. (We could also use the node-voltage method.)

We observe that I = I2 in the top loop, and since I2 is flowing on the outer edge of the circuit, (where there is no circuit on the other side to cause a summation of mesh currents through components), we see that I is also the mesh current for the top loop.

The current mesh equation for the top loop is (the sum of V drops around the loop):

(1)         V2 - I·10Ω + V1 - I (-j100Ω) = 0V

Note:   I must also flow up through C. What I goes down, must come up. (Otherwise, we would accumulate charge in the bottom half of the circuit.)

The mesh current for the bottom loop will be I + I1. This current is flowing on the outside edge of the circuit in the bottom loop.

Our mesh loop equation for the bottom (i.e. sum of V drops around loop) is:

or

Now we use the ideal transformer equations to eliminate all but two unknowns:

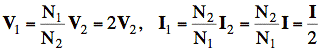
Substituting these into Eq. 1 and Eq. 2 gives two equations in two unknowns:

Now we solve for I. From Eq. 2':

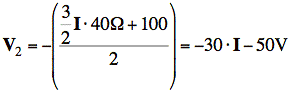
Eq. 1' rearranged is

By substituting for V2, and doing the algebra, we find I:

 

sol'n:  (b)  We use the idea of reflected impedance for a linear transformer:

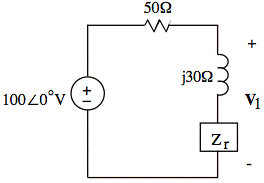
The formula for reflected impedance with a linear transformer is

Here, we have R2 = 0Ω, jωL2 = j20Ω, and ZL = 35Ω + j40Ω.

jωM = j15Ω is the mutual inductance. ∴ ωM = 15Ω

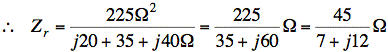
Using the equivalent model for primary side, as shown above, we have

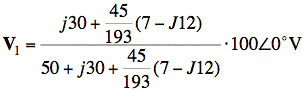
We can factor out a 5 from top and bottom:

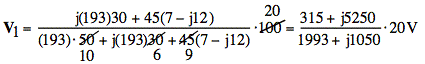
Evaluating the expression and converting to polar form gives