![]() Unit 4
Unit 4 ![]()
2270 PRACTICE EXAM SOLUTION Prob 2
2. (30 points)
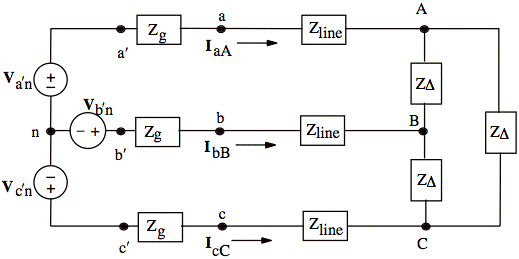
Balanced three-phase, positive-sequence system
IaA = 15 ∠ 0°A Zg = (0.2 + j0.2)Ω
VaA = 22.5 ∠ 53.13°V Z&Delta = (30 + j24)Ω
a. Draw a single-phase equivalent circuit.
b. Calculate IAB.
ans: a)
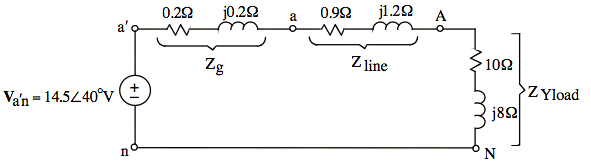
b) IAB = 8.7∠30° A
sol'n: (a) First, we use Ohm's law to find zline
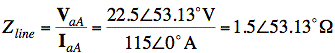
We write zline in rectangular form so we can add it to other impedances later on. Note that zline remains unchanged by any transformations of the source or load from Y to Δ or Δ to Y.
zline = 0.9 + j1.2&Omega
To find the single-phase equivalent, we convert the source end and the load end to Y configurations. Since the source end is already a Y configuration, it remains unchanged.
Zg = 0.2 + j0.2Ω
Transforming the load from Δ to Y results in the load z being divided by 3:
![]()
We now use Ohm's law to calculate the source voltage. Note that IaA is the same for z&Delta as it is for zYload.
![]()
![]()
![]()
sol'n: (b) We first observe that applying Ohm's law translates the problem into one of finding VAB.
![]()
A phasor diagram reveals the relative magnitude and phase angle for VAB versus VAN. When we draw such a diagram, we always start with the shorter side, VAN, and we place it along the real axis. Because this is the most practical way to draw the diagram, we proceed in this fashion even if we are trying to derive VAN from VAB. What the diagram gives us is the relative magnitude and phase angle of VAB compared to VAN. We can then derive a formula that takes us from VAN to VAB or vice versa.
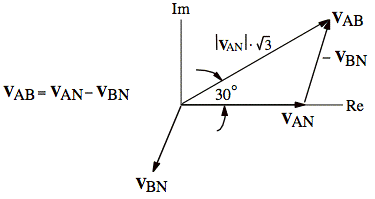
From the diagram, we have
![]()
We find VAN from the single-phase model.
![]()
Substituting into the equation for IAB, we have
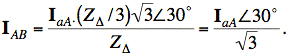
Note: This formula is tabulated in some books, but deriving it ensures that we have the correct sign for the relative phase shift. Whether we shift by +30° or −30° depends on whether we have a positive-phase or a negative-phase system.
![]()