![]() Unit 3
Unit 3 ![]()
2270 PRACTICE EXAM SOLUTION Prob 3
3. (30 points)
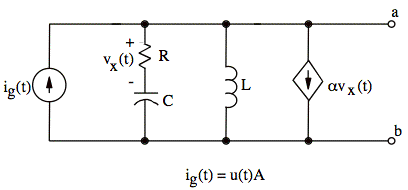
Construct an s-domain Thevenin's equivalent to the circuit at the terminals a-b. There is no initial energy stored in the circuit.
ans:
sol'n: Our s-domain independent current source is
![]()
No initial energy means we may omit the sources that create initial conditions for L and C in the s-domain. Thus, we have just 1/sC and sL:
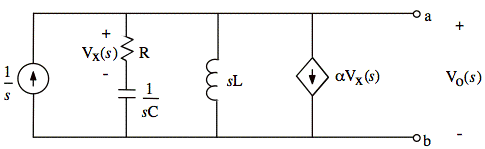
VTh(s) = Vo(s) with no load across a, b terminals.
We use the node-V method to find Vo(s). The first step is to define the dependent current source in terms of node-voltage Vo(s):
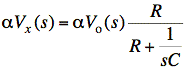
Aside: Another way to deal with the dependent source is to replace it with an equivalent impedance. From the above equation for αVx(s), we can say that the dependent source current is equal to Vo(s)/zeq where
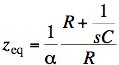
Having replaced the dependent source with this equivalent impedance, we may then calculate Vo(s) as the independent source current times all the impedances in parallel. Also, we observe that the equivalent impedance is valid when the a,b terminals are shorted out. Thus, this approach is a bit more efficient than the standard node-V method.
For the standard node-V method, we have
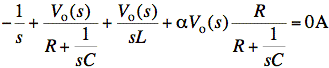
or
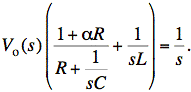
Now we solve for Vo(s) and simplify the result to get a constant times a ratio of polynomials in s with a coefficient of one for the highest power of s in the numerator and denominator. We begin by making each fraction a ratio of polynomials. (We needn't worry yet about the coefficient of the highest power of s.)
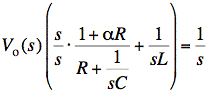
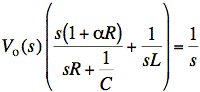
We put the left side over a common denominator and then move the term in large parentheses to the other side:
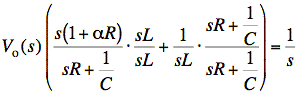
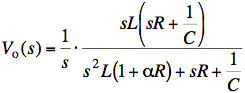
Now we cancel a common factor of s top and bottom and pull out a constant to make the coefficient of the highest power of s in numerator and denominator = 1.
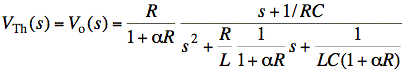
Check: The units of α are 1/R in the original circuit, and that makes αR unitless. √
Check: The units of the numerator of the polynomial ratio are 1/sec. The units for all terms in the denominator are 1/sec2. The units for the constant out front are Ω, and the units for the independent current source are Amps (which were left out to avoid clutter). Thus, the entire expression has units of ΩAsec = Vsec or V back in the time domain. √
Check: If we set R = 0, then we turn off the dependent source and we have
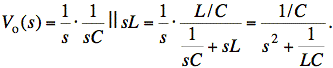
If we plug R = 0 into the formula we derived for VTh(s), we get the same answer. (Note that we multiply through by R in the numerator before setting R to zero to avoid a divide by zero.) √
Check: If we set L = 0, then we short out the output terminals and we have Vo(s) = 0V. If we plug L = 0 into our formula for VTh(s), we get the same answer. (Note that we multiply through by L top and bottom before setting L to zero to avoid a divide by zero.) √
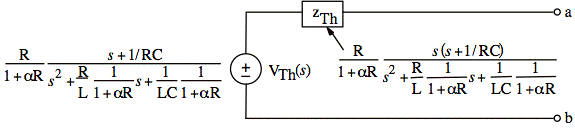
To find zTh, we use the method of measuring the current, Isc(s), that flows through a short across a, b terminals and setting zTh = VTh(s)/Isc(s):

When we perform the same experiment with our actual circuit, all the independent source current flows through the short.
Thus, zTh is just VTh(s) divided by 1/s. This is the same as multiplying VTh(s) by s:
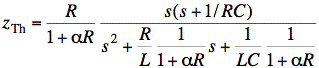
Check: If α = 0, zTh = z looking into a, b with I-source set to zero. (Dependent source disappears when α = 0.)
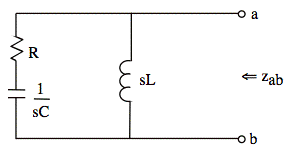
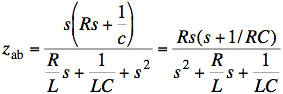
This agrees with our formula for zTh when we plug in α = 0. √
Check: If R = 0, then Vx(s) = 0 and dependent source is off. zTh = z looking into a, b with I-source set to zero.
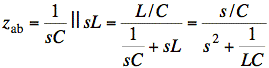
This agrees with our formula for zTh when we plug in R = 0, (R⋅1/RC = 1/C on top). Also, see earlier check of Vo(s) and multiply by s. √
Check: If C = ∞, then 1/sC = 0, Vx(s) = Vo(s), αVx(s) is the same current we would get with R2 = 1/α.
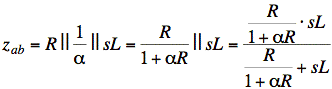
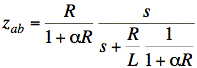
This agrees with our formula for zTh when we plug in C = ∞, (1/∞ = 0). √