![]() Unit 3
Unit 3 ![]()
2270 PRACTICE EXAM SOLUTION Prob 2
2. (45 points)
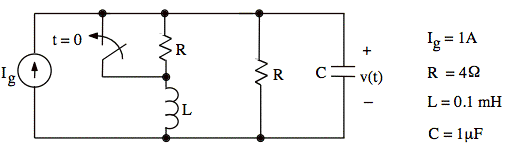
The current source is a dc current source. After being open for a long time, the switch is closed at t = 0.
a. Write a numerical time-domain expression for v(t).
b. From the Laplace transform of v(t), find the numerical values of v(t) for t = 0+ and t → ∞.
ans: a) v(t > 0) = 2.003 e-0.4kt - 0.003 e-249.6kt V
b) v(t = 0+) = 2V, v(t![]() ∞) = 0V
∞) = 0V
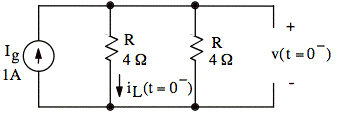
sol'n: (a) First we find initial conditions for L and C. (We need these for s-domain models of L and C.)
For t = 0-, L acts like short, C acts like open circuit.
![]()
![]()
When we close the switch, we short out the first R.
s-domain model:
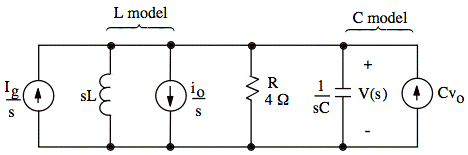
Note: A DC source corresponds to a step function even if there is no switch and the source has the same output for all time. Thus, we have Ig/s as the source in the s-domain. (Conceptually, we only need the current source for t > 0 because the initial conditions on L and C account for what the current source did for t < 0.)
![]()
Note: We may choose either a series sL and V-source for L or a parallel sL and I‑source for L. Here, the parallel I-source model is more convenient. The same applies to the C.
Normally, we might use superposition at this point, turning on the I-sources one at a time and then summing currents or voltages to get a final answer.
Here, however, we have parallel I-sources that sum:
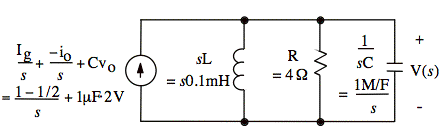
Combining the parallel impedances and using V = Iz, we have
![]()
To compute the parallel z value, we factor out 1/sC to remove fractions:
![]()
Now multiply through by sC:
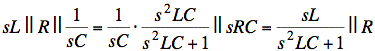
Factor out the denominator again:
![]()
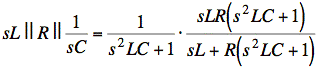
Multiply through by s2LC + 1:
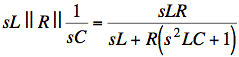
Now divide top and bottom by RLC to make the coefficient of the highest power of s in the denominator equal to unity.

Check: Using the numerator and the first term in the denominator, we have the following units analysis:
![]()
Thus, we have an impedance as we should have. The other terms in the denominator have the same units as s2 since the units of s are, ironically, 1/sec or 1/s.
Now we plug in numbers to compute V(s):
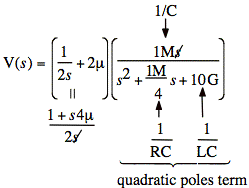
Find poles for quadratic term in preparation for partial fractions:
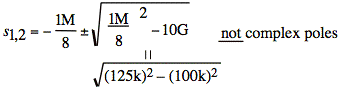
s1,2 = -125k ± 75k rad/s (based on 52 − 42 = 32 pythagorean triple)
s1 = −50k, s2 = −200 rad/s
Now use partial fractions:
![]()
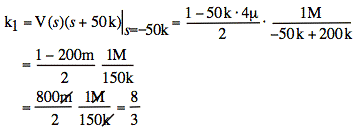
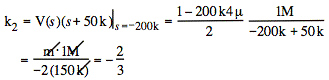
![]()
Use the standard inverse Laplace transform term:
![]()
This gives the final answer:
v(t > 0) = 2.003 e-0.4kt - 0.003 e-249.6kt V
sol'n: (b) Use the initial value theorem to find v(t=0+):
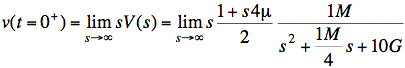
The largest power of s dominates in the numerator and in the denominator.
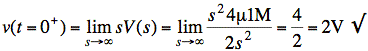
Note: We expect v(0+) = 2V since this is the initial capacitor voltage.
Use the final value theorem to find v(t→∞):
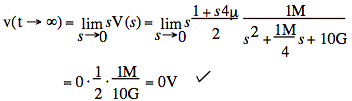
Note: We expect v(t) to decay, since L becomes a short.