Unit 3                                                       

2270                              PRACTICE EXAM SOLUTION Prob 1                                     

 

1.      (25 points)

 

a.       Find f(t) if

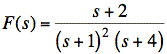
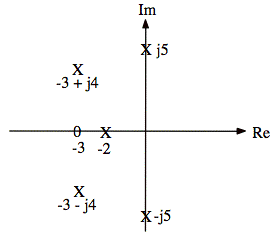
b.       Plot the poles and zeros of G(s) in the s plane

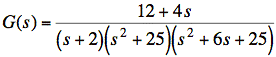
c.      

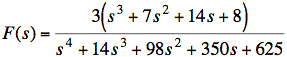
d.      

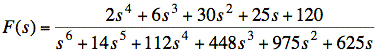
(All poles of F(s) are in the left-half plane.)

e.       Write an expression for H(s).

 

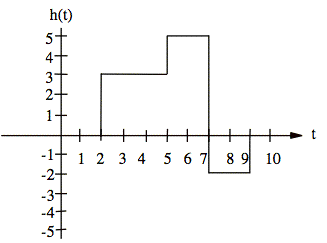
ans:   a)   

b)   

c)     3

d)   

e)    

 

sol'n:  (a)   Use partial fractions.

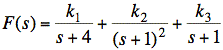
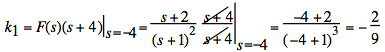
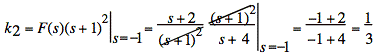
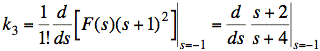
or

or

Plugging in k1, k2, and k3 gives our expression for F(s):

Use inverse Laplace transform for each term to get final answer:

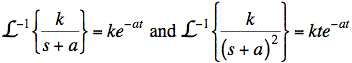
Thus, our answer is

 

sol'n:  (b) 

The zeros are the roots of the numerator, (i.e., the values of s where G(s) goes to zero:

We plot zeros as 0's in s-plane. (See answer plot.)

The poles are the roots of the denominator, (i.e., the values of s where G(s) goes to infinity).

The root for a factor of form s + a is s = -a.

Therefore, poles are at s = −2, −j5, j5, −3 − j4, and −3 + j4.

We plot poles as x's in s-plane. (See answer plot.)

 

sol'n:  (c)   Initial value theorem:

 

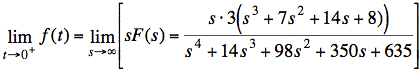
The highest power of s in numerator and denominator dominates as s becomes large. In other words, s2 becomes much larger than s or a constant term as s approaches infinity. Thus, for terms that are summed, we need only consider the term with the highest power of s.

 

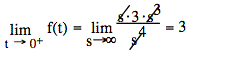
sol'n:  (d)  Final value theorem:

We factor out the highest power of s that is common to every term in the numerator and refer to this as sn. Since we multiply F(s) by s, we always can factor out s1 from the numerator of sF(s). Here, s1 is the highest power of s we can factor out from the numerator of sF(s).

Note:     If the numerator of F(s) ends with a term such as 3s, (for example), then we can factor out s2 from the numerator of sF(s).

We also factor out the highest power of s that is common to every term in the denominator of sF(s) and refer to this as sm. Here, s1 is the highest power of s we can factor out from the denominator of sF(s).

We now write

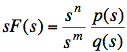
where p(s) and q(s) are polynomials with nonzero constant terms.

In the limit as s→0, we have p(s) = p(0) and q(s) = q(0). We also have sn/sm = 1/sn−m, and we can easily determine the behavior of this term as s→0. The following equation encapsulates these results:

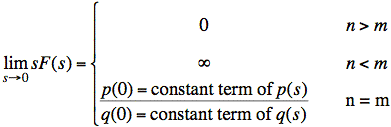
Here,

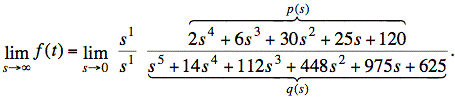
This reduces to

Note:     sn/sm term gives m - n = # poles at origin (net).

if F(s) has two more poles than zeros at origin.

Note:     We must have all poles in the left-half plane. Otherwise, our time-domain solution will contain a term of form eat, a > 0, in f(t). This is a growing exponential that causes

Thus, the first step in applying the final value theorem is to verify that poles are in the left-half plane, (i.e. stable system).

 

sol'n:  (e)   Use delayed step-functions to create windows for piecewise definition of h(t).

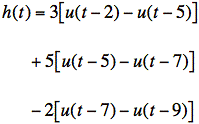
Gather coefficients for each step-function:

or

Now use the identity for delayed functions:

where

Plugging the various values of delay for a, we get our final answer: