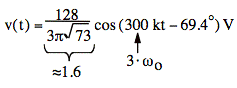Unit 2                                                       

2270                              PRACTICE EXAM SOLUTION Prob 3                                     

 

3.      (30 points)

 

                      

 

                                                

 

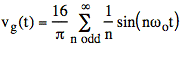
         Write the time-domain expression of v(t) for the first through third harmonics.

 

Ans:    v(t) = 1.6 cos (300k t - 69.4°) V

 

Sol'n:          Summary of steps expanded upon below:

1. We turn each frequency of vg(t) into a phasor.

2. We pass each frequency, kωo, through the circuit by multiplying by the transfer function H(jkωo).

3. The result is the phasor for frequency kωo in the output signal.

4. We convert the output signal phasor back to the time domain, (through the 1st 3 harmonics).

Note: We only have 1st and 3rd harmonics to worry about since we only have odd harmonics in vg(t) and we were only asked to find the output signal's 1st through 3rd harmonics.

1. We turn each frequency of vg(t) into a phasor.

or

or

2. We pass each frequency, kωo, through the circuit by multiplying by the transfer function H(jkωo).

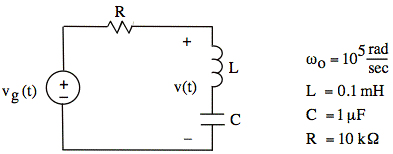
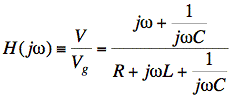(V-divider)

k = 1:

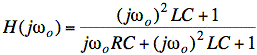
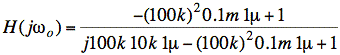
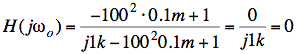
In this case, the L and C together behave like a wire at frequency ωo. The voltage drop across the wire is zero, as is the circuit output. Consequently, H(jωo) = 0.

Note: In this case, the ωo for the vg(t) Fourier series happens to be the same as the center (or resonant, or characteristic) frequency of the L and C:

Typically, the ωo for the Fourier series is different from the ωo for an L and C.

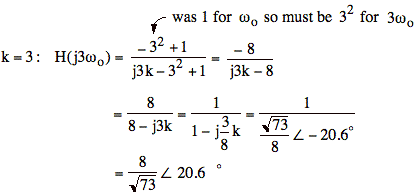
3. The result is the phasor for frequency kωo in the output signal.

Input phasor is

.

Output phasor is

.

4. We convert the output signal phasor back to the time domain, (through the 1st 3 harmonics, of which only the third harmonic is nonzero).