Unit 2                                                       

2270                              PRACTICE EXAM SOLUTION Prob 2                                     

 

2.      (40 points)

         

 

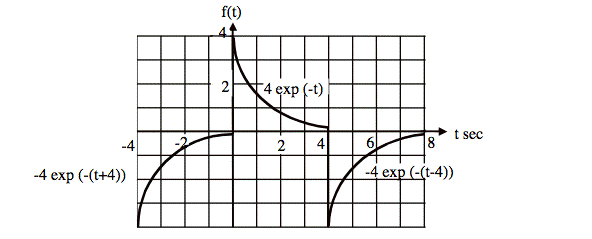
            Find the coefficients for the Fourier series of the above function. The period of the function is 8 sec. From integral tables or a calculator we have:

 

                                   

 

                                   

 

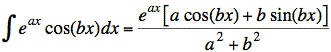
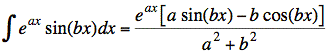
Ans:   

 

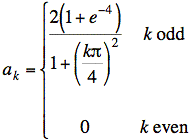
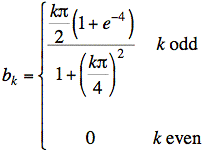
Sol'n:          Since f(t) has equal area above and below the horizontal axis, we conclude that the DC offset is zero: an = 0.

                    Since f(t) is neither even nor odd, we will have nonzero ak and bk terms. f(t) does have shift-flip symmetry, however, so even-numbered terms for ak and bk will be zero. Furthermore, we need only compute integrals over the first half of the function and double them to find values of ak and bk for k odd.

                    We have the following formulas based on shift-flip symmetry:

Using the integrals given in the problem and T = 8, we have (for k odd)

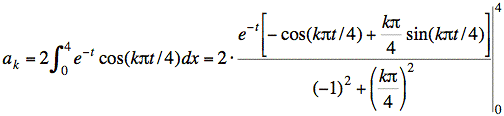
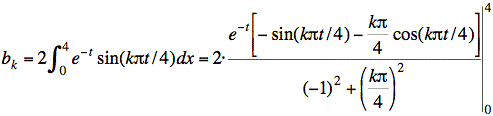
Using sin(0) = 0, sin(kπ) = 0, and cos(0) = 1, and substituting t = 4 for the upper limit, gives

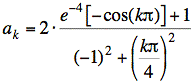
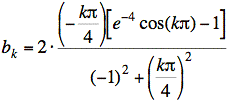
We simplify further by noting that cos(kπ) = −1 when k is odd. With this substitution, we get the final answer.