Unit 2                                                       

2270                              PRACTICE EXAM SOLUTION Prob 1                                     

 

1.      (30 points)

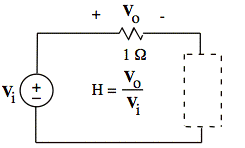
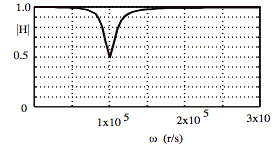
         Using not more than one each R, L, and C, design a circuit to go in the dashed-line box that will produce the |H| vs. ω shown above, that is:

                                                   |H| = 0.5 at ω = 105 rps

                                                   |H| = 1 at ω = 0

                                                   |H| → 1 as ω → ∞

         Specify values of R, L, and C, and show how they would be connected in the circuit. Note that a bandwidth is not specified, and you do not have to satisfy any more than the three requirements specified above.

 

Ans:   

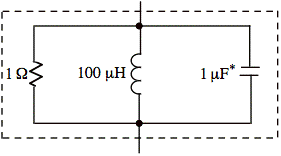
* Any LC = 100 ps is acceptable (if part values are practical).

 

Sol'n:          Given the frequency response plot, we want something resembling a band-reject filter. Since Vo is measured across R1, rather than across the dashed box, we want an L and C configuration that has maximum impedance at resonant frequency. Thus, we need an L in parallel with a C inside the dashed box.

If we denote dashed box by z, we have

(V-divider).    

Note that if

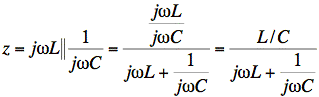
then, at ωo, we have jωL = - .

So 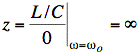at .

Thus, .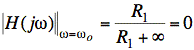

We want a value of 1/2, which we'll correct later on. We do have the desired response at high and low frequencies:

At ω = 0,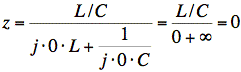             

                           

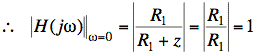
At w®¥,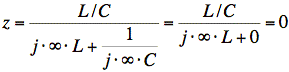            

                           

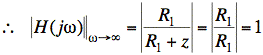
The remaining problem is to add an R2 in the dashed box so that instead of zero. For the parallel L and C, we have

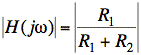at ω = ωo.

If we put R2 in series with the L parallel C, then we would still have z = R2 + ∞ = ∞, at ω = ωo. Thus, we must try something else.

If we put R2 in parallel with L parallel C, then we have z = R2||∞ = R2 at ω = ωo. This gives

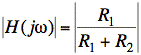at ω = ωo.

We use R2 = R1 = 1Ω to get the required |H(jω)| = 1/2 at ω = ωo.

Now we must verify that we have the correct gain at ω = 0 and ω → ∞. For both cases we have

jωL||1/jωC = 0. The extra R2 in parallel still gives z = 0, as desired.

∴ R2 = 1Ω.

Finally, we need ωo = 105 rad/s (dip in plot). Since we have L parallel C even with the addition of R2, we have the standard resonant frequency:

Therefore, we have

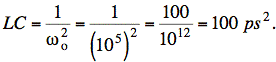
Any LC = 100 ps2 is acceptable unless the L or C are too large or small to be reasonable. For example, one practical solution is

C = 1 μF and L = 100 μH.