![]() Unit 1
Unit 1 ![]()
2270 PRACTICE EXAM SOLUTION Prob 3
3. (50 points)
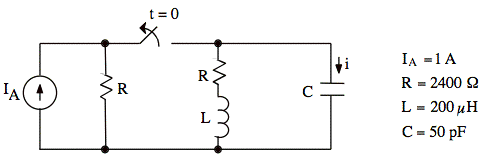
a. After being closed for a long time, the switch is opened at t = 0. Write a numerical time-domain expression for i(t), the current through the capacitance. This expression must not contain any complex numbers.
b. State whether i(t) is underdamped, overdamped, or critically damped.
ans: a) 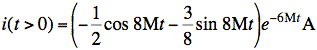
b) Underdamped.
sol'n: (a) When the switch is open, we have series RLC.
![]()
![]()
![]()
![]()
Now find initial condition (i.e. i and di/dt, or v and dv/dt at t = 0+).
Circuit for t = 0-: L's = wires, C's = open circuits.
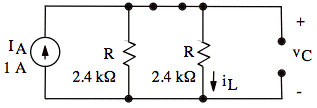
iL(t=0-) = ![]() A (current
divider)
A (current
divider)
![]()
![]() ,
, ![]()
After the switch is open, i = -iL since C and L are in series.
∴ Solve for iL and then change the sign. Note that iL is the variable in the differential equation for a series RLC. Thus, we know how to find it.
We also need
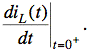
Use V-loop for RLC at t = 0+:
![]()
Note that at t = 0+, (iR = iL since R, L in series),
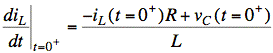
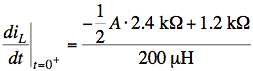
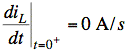
Now use general underdamped solution:
![]()
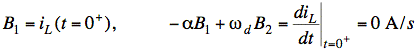
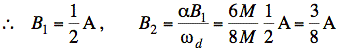
![]()
sol'n: (b) ωo > α ⇒ underdamped