Unit 1                                                       

2270                              PRACTICE EXAM SOLUTION Prob 2                                     

 

2.      (25 points)

 

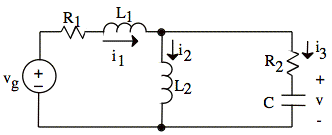
At t = 0, vg(t) switches instantaneously from -vo to +vo.

 

         a.    Write the state-variable equations in terms of the state vector

 

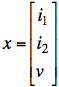
         b.      Evaluate the state vector x at t = 0+.

 

ans:  a)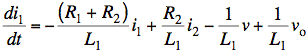    

b)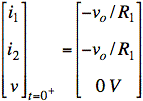    

 

sol'n:  (a)   Our Equations must have the derivative of a state variable on the left and only state variables and constants on the right.

Find an equation for di1/dt from vL1 = L1 di1/dt or di1/dt = vL1/L1. Similarly, di2/dt = vL2/L2.

We find an equation for dv/dt from iC = C dv/dt.

The diagram below shows the polarities of vL1, vL2, and iC. It also shows a reference and node voltage.

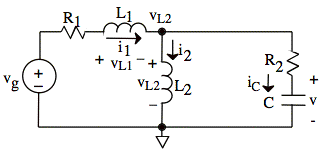
We treat L1 and L2 as current sources and v as a voltage source, and we solve for vL1, vL2, and iC using standard techniques (such as node-voltage or superposition). Each variable we are solving for is the voltage for a current source or the current for a voltage source. Thus, they are variables we solve for indirectly: we solve the circuit and then use Kirchhoff's laws to find the value we are looking for in terms of other values.

Since the current through R2 is i1 − i2, we may solve for node voltage, vL2, directly in the above circuit: (We could also use the node-voltage method.)

This happens to be one of the variables we wish to solve for, and we find the equation for di2/dt by dividing the equation by L2.

or

We derive vL1 from a voltage loop on the left.

We find the equation for di1/dt by dividing the equation by L1 and substituting vo for vg.

or

We derive iC from a current summation at the top node.

We find the equation for dv/dt by dividing the equation by C.

or

sol'n:  (b)  We find initial conditions by looking at the circuit at time t = 0−. Because we are dealing with state variables, (i.e., energy variables), their values cannot change instantly and will be the same at time t = 0− and t = 0+.

At time t = 0−, the circuit has reached equilibrium; voltages and currents are no longer changing; derivatives are zero; vL = L diL/dt = 0 and iC = dvC/dt = 0. Thus, the inductors look like wires and the capacitor looks like an open circuit.

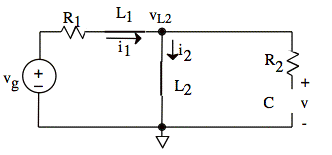
Since no current flows through R2, we may find i1 (which equals i2) from the loop on the left side.

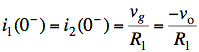
Since no current flows through R2, there is no voltage drop across R2. Thus, v equals the voltage drop across the wire representing L2. In other words, we have

The state variables have the same value at time t = 0+ as at t = 0−.