Unit 1                                                       

2270                              PRACTICE EXAM SOLUTION Prob 1                                     

 

1.      (25 points)

 

                                    

 

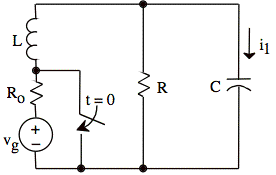
                        vg is a dc voltage source

                        After having been open for a long time, the switch is closed at t = 0.

         a.      Give expressions for i1(0+) and i1´(0+), (i.e., di1/dt at t = 0+), in terms of no more than vg, Ro, R, L, and C.

         b.      For L = 10 μH, choose R and C so that the system is underdamped and

                  α = 3⋅106 rad/s, ωd = 4⋅106 rad/s.

 

ans:  a)     i1(0+) = 0A

                 

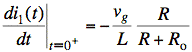
         b)     C = 4nF, R = 41.7Ω

 

sol'n:  (a)   To determine what the L and C are doing at t = 0+, we find the value of iL(t = 0−) and vC(t = 0−) and argue that these values will be the same at time t = 0+, since they cannot change instantly.

We find iL(t = 0−) and vC(t = 0−) from circuit model for t = 0-: L acts like wire, C acts like open.

 

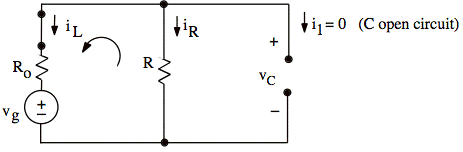
Current circulates only in the left inner loop, meaning iL = −iR. The current in this loop is just the source voltage divided by the sum of R and Ro.

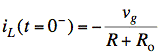
The right side looks like two dangling wires carrying no current but measuring the voltage drop, vC, across R. The voltage drop is given by the voltage divider formula for R and Ro across vg.

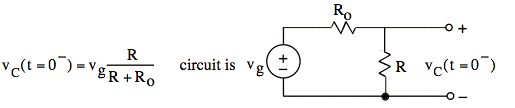Since iL and vC cannot change instantly, we have

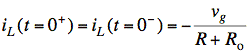
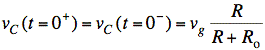
The instant after the switch is closed, we model the inductor as a current source and the capacitor as a voltage source:

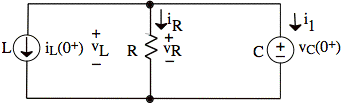
Henceforth, we work towards final answers involving only the state variables iL and vC. Since these are the only sources in the circuit, our answers will be in terms of state variables if we solve the circuit using standard techniques such as node-voltage.

If we place a reference on the bottom center node, then the top center node voltage is vC(0+), owing to the voltage source on the right. Since i1 is a current flowing through a voltage source, we find its value by summing currents out of the top-center node.

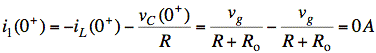
This answer seems suspicious because the current before t = 0+ was zero, too, and something has to change... The answer is correct, however, because the inductor and resistor currents have not changed. They are both determined by state variables that have not changed.

Qualitatively, what happens in this circuit is that iL cannot change instantly when the switch closes. Before the switch closes, R carries all of iL (because C acts like open circuit). After the switch closes, iR cannot change instantly (because vC is across R and vC cannot change instantly). Thus, R still carries iL just after the switch closes. This implies that i1(0+) = 0.

To find the derivative of i1 at t = 0+, we differentiate the equation for i1 in terms of state variables found above and plug in t = 0+ after we differentiate. (Note that, if we differentiate iL(0+), then we are differentiating a constant and we get zero.)

We convert these derivatives of state variables back into variables that are not derivatives by rearranging basic component equations for L and C:

We have

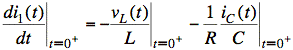
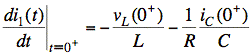
Returning to the circuit diagram for t = 0+, we solve for vL(0+) and iC(0+) using standard methods. In this case, we have vL(0+) = vC(0+) and iC(0+) = i1(0+). Plugging in these known values, we have

 

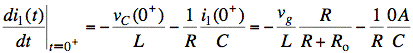
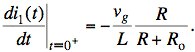
sol'n:  (b)  α = 3 M/s = 1/(2RC) for parallel RLC

underdamped RLC

Thus, ωd2 = 42 M2/s2 = ωo2 − 32 M2/s2.

From 32 + 42 = 52 Pythagorean triple we have

Now use the definition of alpha