![]()
![]()
2270 PRACTICE FINAL EXAM SOLUTION Prob 4
4. (50 points)
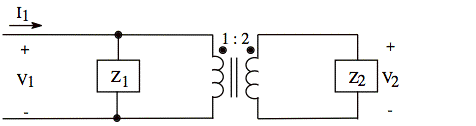
Z1 = (5 - j5)Ω Z2 = (20 + j20)Ω
a. Find the input impedance, zin = V1/I1, for the above circuit.
b. Using zin from (a), find a numerical expression for VAB in the circuit below.
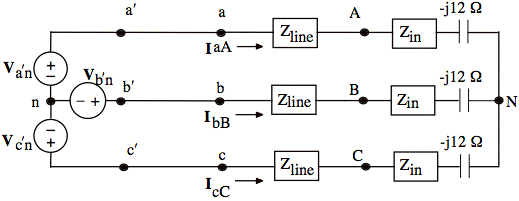
Balanced three-phase system.
Van = 52 ∠ 0°V Vbn = 52 ∠ −120°A zline = j12 Ω
ans: a) zin = 5 Ω
b) VAB ≈ 234∠−37.38° V
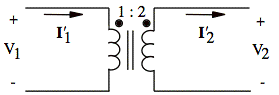
sol'n: (a) Transformer
is ideal. To distinguish currents in the transformer itself from other
currents, we use a prime to denote the transformer currents. The current
flowing into the dot on the primary side is ![]() , and the current
flowing out of the dot on the secondary side is
, and the current
flowing out of the dot on the secondary side is ![]() :
:
![]()
Using the above model, we can derive the formula (or we can just look up the formula) for secondary impedance reflected into the primary:
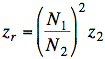
Our model, given N1/N2 = 1/2 turns ratio, is:
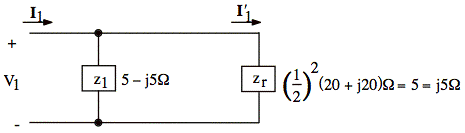
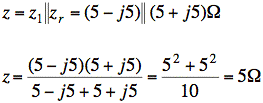
sol'n: (b) Our first step is to convert our circuit to a Y − Y form so we can use a single-phase equivalent model. In this problem, the circuit is already in Y − Y form and we may draw the single-phase equivalent directly:
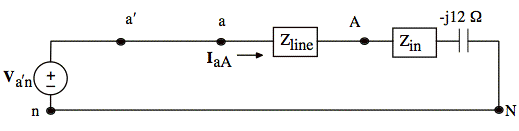 We find VAN and
then calculate VAB using phasor diagrams. We obtain VAN from
the voltage divider formula:
We find VAN and
then calculate VAB using phasor diagrams. We obtain VAN from
the voltage divider formula:
![]()
![]()
![]()
We use a phasor diagram to relate VAN to VAB. The diagram shows the relationship between VAN and VAB, and we assume VAN has phase angle zero so we can find the relative phase angle of VAB.
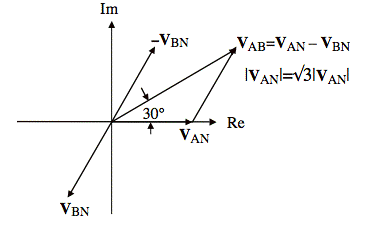
From the diagram, we deduce that
![]()
Plugging in the value of VAN gives the numerical value of VAB.
![]()
VAB ≈ 234∠−37.38° V