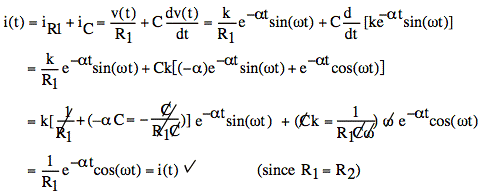2270                       PRACTICE FINAL EXAM SOLUTION Prob 3                              

 

3.      (50 points)

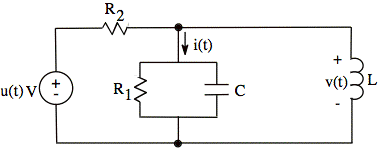
The initial energy stored in the circuit is zero.

R2 = 500 Ω                     L = 200 mH

a.   Choose values of R1 and C to accomplish the following:

(1)   v(t) and i(t) are decaying sinusoids 90° out of phase with each other.

(2)   1/α = T, where α is the exponential decay constant and T is the period of oscillation of the decaying sinusoid.

b.   With the component values you chose in the circuit, write numerical expressions for v(t) and i(t).

 

ans:  a)     R1 = 500Ω, C = 32.4 μF

         b)     v(t) = 159 e-61.7t sin(388t) mV

i(t) = 2 e-61.7t cos(388t) mA

 

sol'n:  (a)   This problem could actually be solved by solving the RLC problem with the general solution to the differential equation for a parallel RLC (obtained by taking the Thevenin equivalent of the voltage source and two resistors). The Laplace transform approach is a bit more straightforward, however, and would also work for input sources other than a step function.

We begin by Laplace transforming the source and circuit components. Since no initial energy is stored in the circuit, we have no extra current or voltage sources in the component models. In general, we would have to include such sources to account for the initial conditions.

s-domain model:

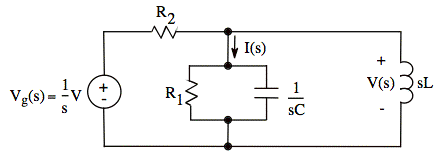
First, we find V(s). We can then find I(s) from V(s) using Ohm's law.

Our calculations are cleaner if we use a Thevenin equivalent for Vg(s), R1, and R2.

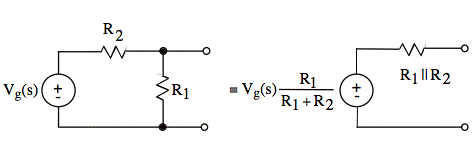
Note: After we replace Vg(s), R1, and R2 with the Thevenin equivalent, we no longer have a point in the circuit where I(s) is flowing. Nevertheless, we may still compute I(s) from V(s):

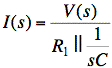
(Note that V is across R1 and 1/sC as well as across sL.)

Our circuit model becomes:

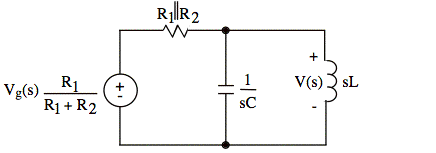
The impedance of the L and C in parallel is

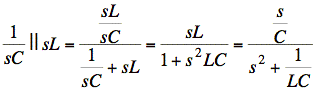
Use V-divider to find V:

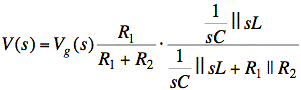
Now simplify the expression.

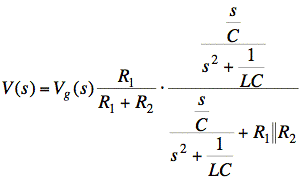
Multiply top and bottom by s2 + 1/LC:

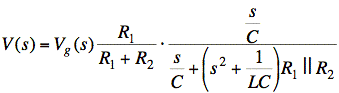
Rewrite the voltage divider as R1||R2/R2:

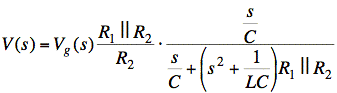
Divide top and bottom by R1||R2:

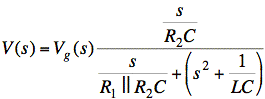
Tidy up the denominator and substitute Vg = 1/s:

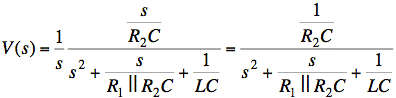
V has the form of a decaying sine wave:

where k is a real constant and

Aside:  The fundamental form of the polynomials appearing in V(s) is independent of the value of R1, R2, L, or C. If I(s) is to be 90° out of phase with V(s), we must hope that it can be made to have the form of a decaying cosine:

where k2 is a real constant (positive or negative).

I(s) is V(s) divided by the parallel impedance of R1 and C:

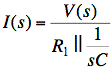
The parallel impedance of R1 and C is

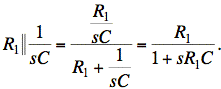
Substituting for V(s) gives

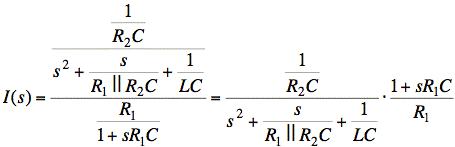
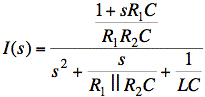
Above, we concluded that I(s) must be of form

The denominator polynomial in s is in the correct form. Matching the numerators gives:

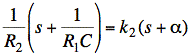
We must have k2 = 1/R2 and α = 1/R1C. Earlier, we found

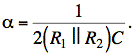
We conclude that

The solution to this equation is R1 = R2 = 500 Ω, (value given in problem statement):

A standard value for R1 would be 510 Ω.

Now we find C. We look for an equation with C as the only unknown. The problem states that 1/α = T or α = 1/T = ω/2π:

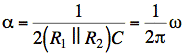
From the constant term in denominator of V(s) and I(s), as noted earlier, we have an equation involving α and ω:

Substituting for α and ω, we have

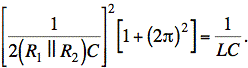
Inverting both sides, we have

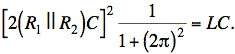
Rearranging and canceling one power of C on both sides gives a value for C:

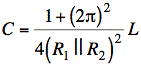
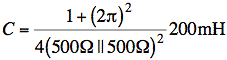
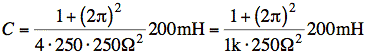
A standard value for C would be 33 μF.

 

sol'n:  (b)  From (a) we know

From (a) we also know

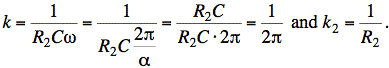
Note: We use 1V in the numerators because Vg(t) actually transforms to 1V/s rather than 1/s. We leave out the 1V to avoid clutter and confusion in the calculations. We might mistakenly think of the 1V as V(s).

For α and ω, we have

Substituting numerical values for k, k2, α, and ω in the time-domain forms for i(t) and v(t) gives our final answer.

v(t) = 159 e-61.7t sin(388t) mV

i(t) = 2 e-61.7t cos(388t) mA

Consistency check: