![]() Unit 2
Unit 2 ![]()
1270 PRACTICE EXAM SOLUTION Prob 1
1. (a) (10 points)
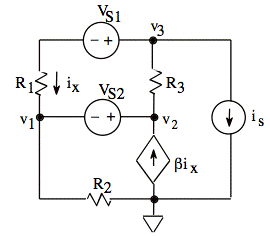
For the circuit shown, write three independent equations for the node voltages v1, v2, and v3. The quantity ix must not appear in the equations.
(b) (10 points)
Make a consistency check on your equations by setting one or more resistor values to 0 or ∞ and setting other sources and resistor to values for which v1, v2, and v3 are obvious.
(c) (10 points)
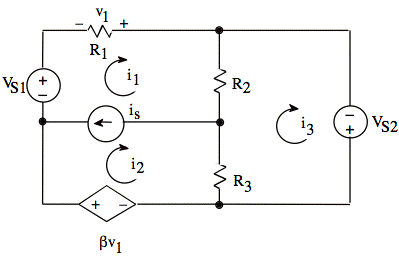
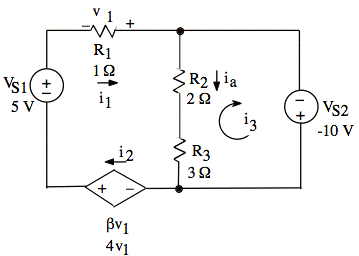
For the circuit shown, write three independent equations for the three mesh currents i1, i2, and i3. The quantity v1 must not appear in the equations.
(d) Make a consistency check on your equations by setting one or more sources to zero and using convenient resistor and source values.
Solution:
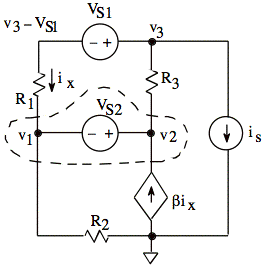
We have a supernode, (dashed box on diagram, above), since v1 and v2 are connected by a V source. Sum of currents out of both nodes = 0 A:
![]()
v1 and v2 are related by V drop between them:
![]()
Now we need the node-V equation for v3:
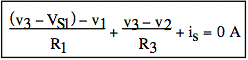
Now we eliminate ix by expressing it in terms of node voltages:
![]() substitute into
the first equation to get:
substitute into
the first equation to get:

(b) Consistency checks. Choose convenient source and R values, and verify that the equations are satisfied.
Check:
![]() disconnected
disconnected
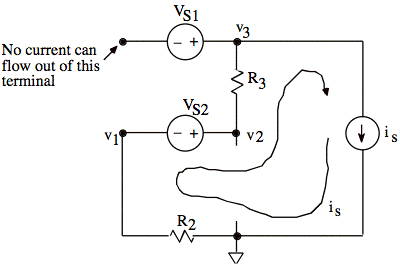
We observe that is flows around the entire loop. Therefore,
v1 = -isR2
v2 = v1 + VS2 = -isR2 + VS2
![]()
Plug v's into our answer to (a):
1) ![]()
![]()
2)
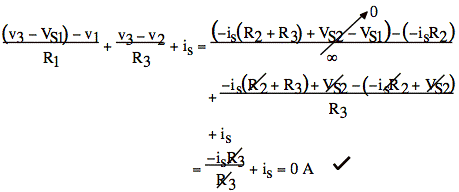
3)
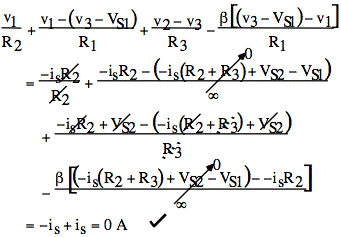
or Check: R3 = ∞ Ω and VS1 = 0 V and VS2 = 0 V and is = 1 A
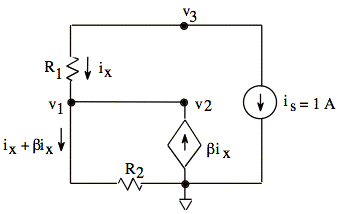
ix = -is = - 1 A
v1 = ix(1 + §)R2 = (-1 A)(1 + §)R2
v2 = v1
v3 = v1 + ixR1 = (- 1 A)[(1 + §)R2 + R1]
Plug v's into our equations from (a)
1) v2 - v1 = v1 - v1 = 0 = VS2 ![]()
2)
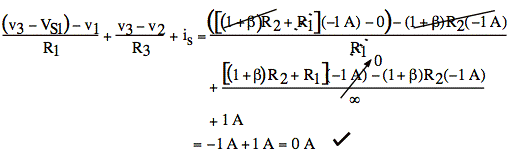
3)
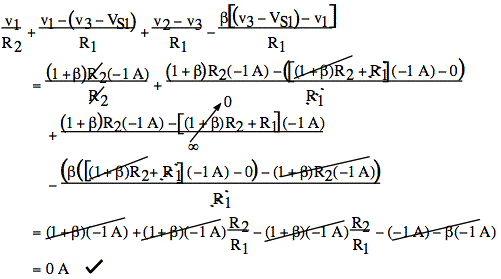
Note: It is probably easier to choose actual numerical values for all the components. Where possible, you may wish to use values that are easy to work with and can be uniquely associated with a component.
R1 = 1 Ω, R2 = 2 Ω, R3 = 3 Ω, is = 4 A, VS1 = 5 V, VS2 = 10 V, for example.
We might choose § = 9 so we get 1 + § = 10, for convenience.
We might also choose to avoid multiplying numbers, and instead try to cancel out terms as in the above solution.
P.S.: I found an error in my solution to (a) from the consistency checks performed above. It works!
(c)
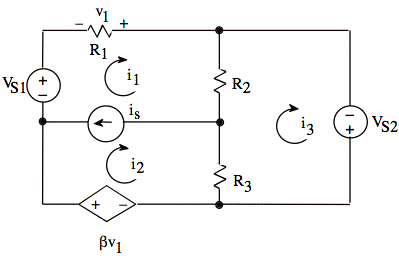
We have a supermesh where the is source is located. We go around the outer loop containing is.
![]()
We observe that we have constraint equation v1 = -i1R1. Substitute this constraint into the first equation to eliminate v1:
![]()
We need one more constraint equation. It arises from the current source we left out of the supermesh equation
![]()
For i3 mesh loop, we have:
![]()
1. (d) Consistency checks.
Check: VS1 = 0 and VS2 = 0 and § = 0 and R1 = 1 Ω, R2 = 1 Ω, R3 = 3 Ω and is = 5 A.
We may redraw the circuit R1 shorted by the wire on the right. When drawn this way, i3 flows up on the right outside edge.
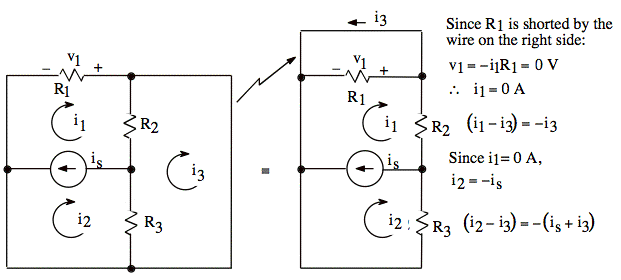
Only i1 flows through R1, and i1 = 0. Therefore, we may remove R1.
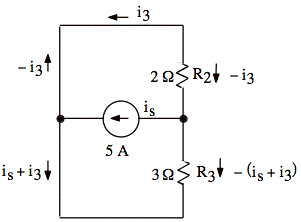
We have a current divider.
![]()
![]()
i1 - i2 = is ![]()
Plug i's and R's into our answer to (c):
1)
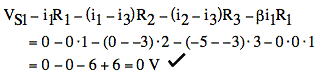
2)
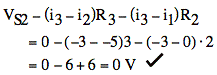
3) ![]()
![]()
Or check: is = 0, R1 = 1 Ω. R2 = 2 Ω. R3 = 3 Ω. VS2 = - 10 V, VS1 = 5 V, § = 4
10 V across R2 + R3 = 5 Ω
![]()
![]()
But
![]()
![]()
or
![]()
![]()
![]()
Plug into equations from (c)
1)
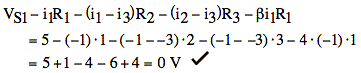
2)
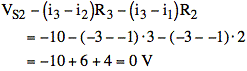
3)
![]()
Note: We have to be very careful about consistency checks that change the circuit topology. One helpful fact is that if a mesh loop has one side that is on the edge of the circuit diagram—so only one mesh current flows in it—then we are safe in saying the current in that component is equal to that mesh loop current. Thus, we look for components on the perimeter of the circuit when we do consistency checks.