![]() Unit 1
Unit 1 ![]()
1270 PRACTICE EXAM SOLUTION Prob 4
4. (30 points)
The op amp operates in the linear mode. Using an appropriate model of the op amp, derive an expression for vo in terms of not more than is, R1, R2, and R3.
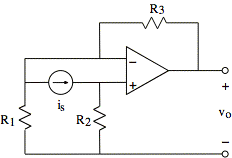
ans: ![]()
sol'n: Using passive sign convention, label voltage drop and current measurement polarities.
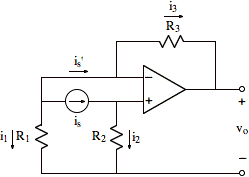
Assume an ideal op-amp since we are in linear mode and we are solving for DC conditions.
Use the standard procedure to find vo:
1) Calculate the voltage drop, vp, from the Ð input of the op amp to the bottom wire, (i.e. across R2). We use Kirchhoff's law for summation of currents out of the node next to the + terminal of the op-amp. Since ip = 0, (i.e., no current flows into the + terminal), we conclude that
i2 = is.
By Ohm's law, it follows that
vp = isR2
2) Remove the op amp, put a source called vo across the terminals where we measure the output, and assume a 0V drop from + input to Ð input of op amp. (Because of negative feedback, the op-amp output voltage, vo, reaches an equilibrium level that results in a nearly 0V drop from + input to Ð input.) Now we have the following model circuit:
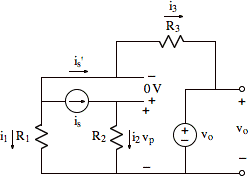
Note that we model the Ð terminal of the op-amp as a voltage source with zero current flowing into it. We add this constraint on the current with the understanding that vo must have a value that results in in = 0.
3) Calculate is', the current flowing toward the Ð terminal from the left. Note that current is' has a name similar to the current source only by coincidence.) Now we observe that the voltage drop from the Ð terminal of the op amp to the bottom wire is vp Ð 0V = vp. It is as though we have a voltage source of voltage vp from the Ð terminal of the op amp to the bottom wire. This voltage source separates the two sides of the circuit. What happens on the right side of the circuit will not affect the value of is'. Thus, we utilize the left side of the circuit to calculate is'.
We use a summation of node currents at the node above R1 to calculate the value of is':
is' + i1 + is = 0 or is' = Ð(i1 + is)
But we can also calculate i1 because we have vn across R1:
i1 = vp/R1 = isR2/R1
We can now solve for is':
is' = is(R2/R1 + 1) = is(1 + R2/R1)
4) Calculate i3, the current flowing in the negative feedback path on the right side of the circuit. Again, it is as though we had a voltage source of voltage vp from the Ð terminal of the op amp to the bottom wire. We utilize this voltage source and a voltage loop around the right side of the circuit to calculate vo:
vp Ð i3R3 Ð vo = 0 or i3 = (vo Ð vp)/R3 = (vo - isR2)/R3
5) Since in = 0, set is' = i3.
is' = is(1 + R2/R1) = i3 = (vo - isR2)/R3
Equate the 2nd and 4th expressions and solve for vo.
is(1 + R2/R1) = (vo - isR2)/R3 or vo = isR3(1 + R2/R1) + isR2 or
vo = is(R2 + R3 + R2R3/R1)
Consistency checks:
1) By linearity and
fact that we have one source, is, we expect vo
to be directly proportional to is. Agrees with our formula for vo. ![]()
2) Consider R2 = 0: Then vp = 0. Therefore, i1 = 0 and i3 = -is. Then, vo = -i3R3 = isR3.
Agrees with our formula for vo when we plug in R2 = 0. ![]()
3) Consider R1 = ° (open circuit): vp = isR2, i3 = -is, and vo = vn Ð i3R3
= isR2 + isR3. Agrees with our formula for vo when we plug in R1 = °. ![]()
4) Consider
R3 = 0: Then vo = vn = vp = isR2.
Agrees with our formula for vo
when we plug in R3 =
0. ![]()