|
|
Unit 1 |
|
|
|
PRACTICE EXAM SOLUTION Prob 3 |
1270
3. (30 points)
a. Derive an expression for i2. The expression must not contain more than the circuit parameters ß, Va, ia, R1, and R2.
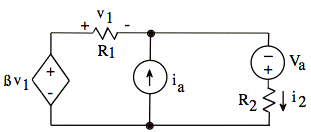
b. Make at least one consistency check (other than a units check) on your expression. Explain the consistency check clearly.
ans: a) 
b) Many possible answers. See solution below.
sol'n: (a) Use Kirchhoff's laws to write several equations. Then eliminate unwanted variables.
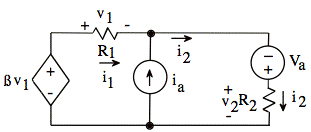
We sum currents out of top-center node:
–i1 – ia + i2 = 0
Note that summing currents out of bottom-center node does not give us anything new. By Ohm's law, we also have
Now, we sum voltages around a loop. We choose the outer loop because the inner loops have a current source with unknown voltage drop.
By Ohm's law, we also have
After the Ohm's law substitutions, we have two equations, and we may eliminate v1.
Use the simpler equation first:
or v1 = (i2 – ia)
Substitute for v1 in the second equation:
After some algebra, we get
units consistent
(b) There are many possible consistency checks.
1) ia = 0 and R1 = 0. Then v1 = 0, ßv1 = 0, and sum v's around outer loop gives i2 = Va/R2. Our formula also gives Va/R2. 
2) Consider R1 = 0 and R2 = 0. As in (1), v1 = 0 and ßv1 = 0. Since R2 = 0 we also end up with a short across Va:
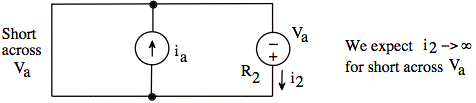
Our formula gives
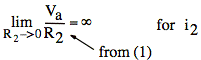
3) Consider ia = 0, ß = 0:
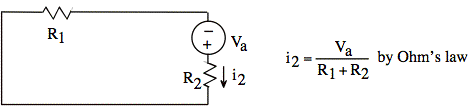
Our formula gives
4) Consider 
(open circuit)
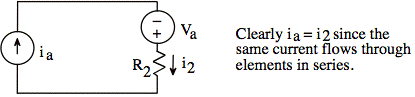
Our formula gives:
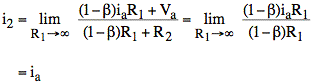
5) Consider
(open circuit): We
have i2 = 0 since no
current flows through the open circuit. Our formula gives:
Many more consistency checks are possible.