Unit 1                                                       

1270                              PRACTICE EXAM SOLUTION Prob 2                                     

 

2.      (30 points)

 

         Derive an expression for i3. The expression must not contain more than the circuit parameters Va, Vb, ia, R1, R2, and R3.

 

                             

 

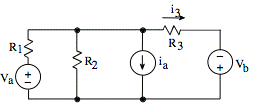
ans:     

 

sol'n:  Using passive sign convention, label voltage drop and current measurement polarities.

 

 

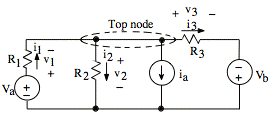
      Use Kirchhoff's laws:                   

                                                      sum v drops around loop = 0

                                                      sum i out of node = 0

 

      v drops for loop on left, using Ohm's law for v1 and v2:

 

                                                            

 

      Middle loop would include current source, so use slightly larger loop with R2 on left and Vb on right:

 

                                                           

 

      Now sum currents out of top node (that consists of the two top nodes connected by a wire). Note: We are always allowed to combine nodes connected by wires.

 

                                                             -i1 + i2 + ia + i3 = 0 A

 

      We now have three equations in three unknowns. We solve for i3. Use the second equation to eliminate i2:

 

                                                                  

 

      Use the first equation to eliminate i1:

 

                          

 

      Substitute for i1 and i2 in the third equation:

 

                                       

 

      Solve for i3:

 

                                    

 

                                            

 

      Multiply both sides by R1R2 to clear fractions:

 

                               

 

      or

 

                                                  

        

         Now for consistency checks to verify our answer. (Optional)

1)      Consider ia = 0, Vb = 0, and R3 = 0:

                                

 

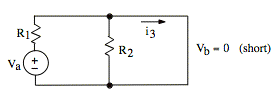
         Since R2 is bypassed by a short, no current flows in R2. Therefore, we can remove R2 without changing i3:

 

                           

 

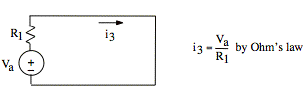
         Our formula gives i3 = .

 

2)      Consider ia = 0 (open circuit) and R2 = ¥ (open circuit):

 

         Removing R2 and ia leaves total voltage Va + Vb across R1 + R3 in outside loop.

 

         Therefore, we have

 

                                                                  

 

         For our formula, we use the following identities:

 

 

         Making these substitutions in our formula gives

 

                                                             

 

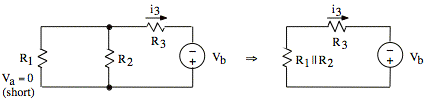
(3)    Consider Va = 0, ia = 0:

 

                                                                

 

         Our formula gives or .

 

(4)    Consider Va = 0, Vb = 0:

 

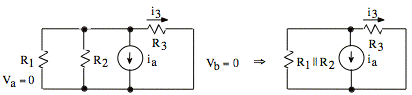
         By current divider formula, we have .

 

         Our formula gives or

 

(5)    Consider ia = 0, Vb = 0.

                    

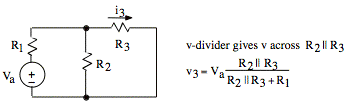
         Now

                                                                              

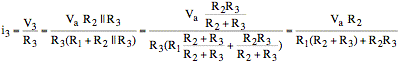
         Our formula gives .