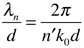Assignment 2
Assignment
Starting from your assignment 1 project file, change the block material FR-4 (lossy) to Teflon (PTFE)(lossy), a very useful polymer. Do this by right-clicking the object in the Navigation Tree and choosing Change Material.... If you used the default name this object will be called solid1.
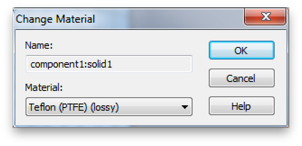
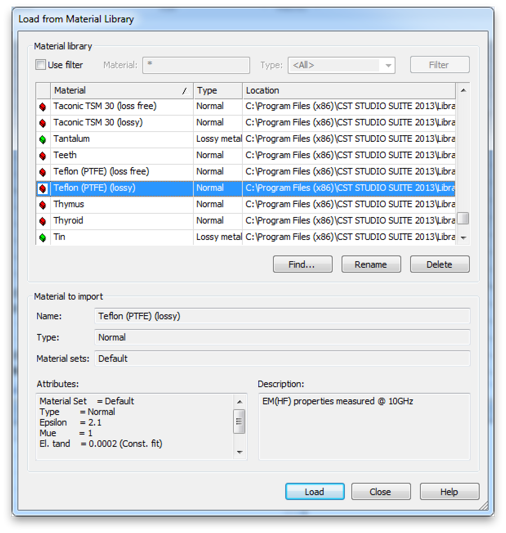
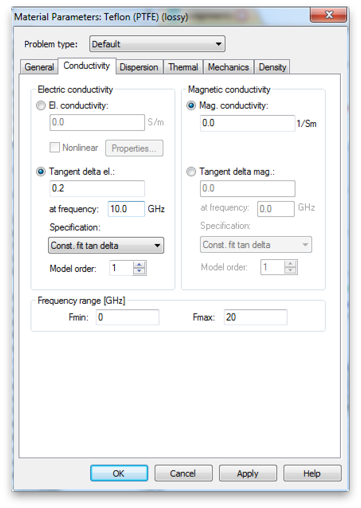
To make the material a bit more interesting, increase the electric tan delta from 0.0002 to 0.2. Double-click the Teflon (PTFE)(lossy) entry in the Materials folder of the Navigation Tree. Then click the Conductivity tab and make the change. (This does not change the material library just the instance of the material used in this project.)
Lets also change to using our own vacuum spacing rather than relying on open (add space) to do so automatically. (This is generally a good idea.) Change the z boundary conditions to open.
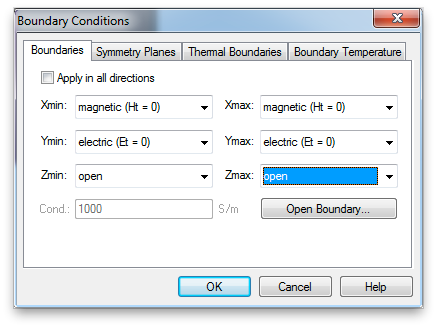
Then add a vacuum block the encompasses the Teflon block and adds 5mm of space to both ports.
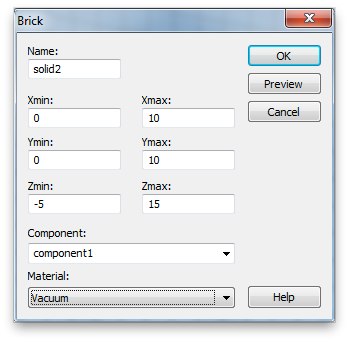
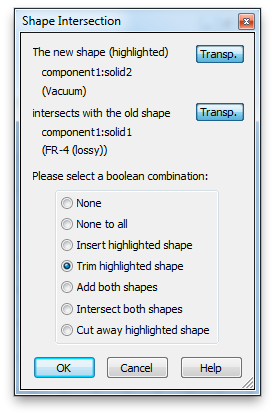
After clicking OK, the program will want to know how to handle the intersection of the the Teflon block and the vacuum brick. We want to trim the vacuum brick.
Adjust the Distance to Reference Plane correctly for the new spacing.
After making significant changes to the structure you should re-run adaptive meshing. Before doing this, reset the mesh parameters to the default values of 10 Lines per wavelength and 10 for the Lower mesh limit. These properties area accessed through the Global Mesh Properties panel on the Simulation tab.
Run the sim with accuracy and port excitations as in assignment 1.
Export the S-parameters, and also, export the modified Teflon material properties.
-
1.Using the formulas from the Smith paper attempt to extract the material properties from the S-parameters. You will first calculate n and Z, and then from them, mu and epsilon. Make branch corrections as discussed in class. Submit plots comparing the real and imaginary part of the extracted mu and epsilon with the corresponding model properties used in the simulation. Make one plot without branch corrections and one with. (For the permeability the model properties are 1+0*j.)
-
2.How is the agreement?
Now lets try a structure for which we do not know the effective medium material properties in advance. Put a sphere of Silicon in the center of the Teflon block. Use the Sphere tool from the Modeling tab and hit escape to pull up the numerical entry window. Make the sphere Center radius 3mm. (The Top and Bottom radius should be zero.) Choose [Load from Material Library..] from the Material menu and select the Silicon (lossy) material.
After clicking OK, the program will want to know how to handle the intersection of the the Teflon block and the silicon sphere. material. We want to insert the sphere into the block.
If you click the Silicon (lossy) material in the Materials folder of the Navigation Tree, you should see:

Now run the simulation. Again, you usually want to reactivate the adaptive mesh refinement when making a significant structure change like this. Reset the global mesh properties to the 10/10 values first, otherwise the you will start from the previous adaptations mesh which is not particularly relevant for the new structure.
You might guess that an analytical model for the effective material properties exists for such a simple structure. In fact there are many with varying degrees of sophistication. Perhaps the simplest is the Maxwell-Garnett equation, equation 7 at this wikipedia link.
-
3.Calculate the volume fraction of the silicon sphere.
-
4.Use the exported Teflon properties, the silicon properties (which you can assume are constant and lossless) and the volume fraction to calculate the Maxwell-Garnett effective permittivity. Also calculate the effective permittivity and permeability from the simulation S-parameters using the Smith article equations as before. (Dont bother with branch correction on this part. We will only be concerned with the low frequency region where the default branch is correct.) Plot the real and imaginary parts of the permittivity versus frequency for both these results on the same graph to compare. Make another graph for the permeability. (Since both the block and sphere are non-magnetic, the Maxwell-Garnett permeability is, of course, 1+0*j ).
-
5.Find the maximum frequency for which the Maxwell-Garnett material properties (both the complex permittivity and permeability) agree with the S-parameter extracted material properties to within 3%. Calculate the effective medium parameter at this frequency