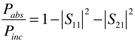Assignment

In this assignment, we will find the S-parameters of a slab of FR-4 by performing a time domain simulation. We will find these S-parameters with the default phase reference (incorrect) and with the phase reference de-embedded to the FR-4-vacuum interface (correct). Then we will compare the simulation results with an analytical formula.

Launch CST Studio Suite (from the desktop.) Accept the university version agreement.

Open CST Microwave Studio, the icon in the lower left corner.

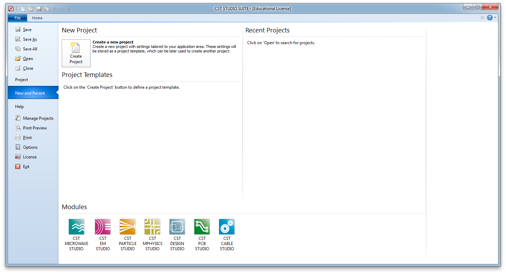
Then select Do no use a project template and click OK.

Let’s set up a few basic things, before we do any modeling.

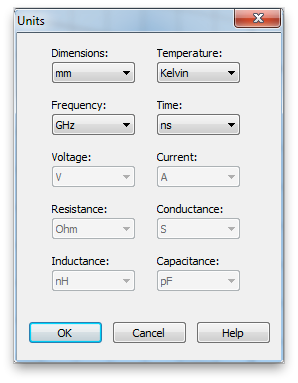
Click the Home tab, then click Units on the command ribbon. Set the units to mm, GHz and ns (nano-seconds). These will be most convenient units for the scale we will be working at.

Next select the Simulation tab, and click Frequency.  Set the maximum frequency to 20 GHz.

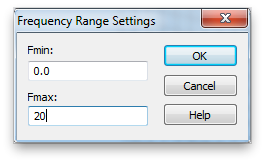
Click Background. Set the background material to Normal, instead of PEC. The values for the background Epsilon and Mue can be adjusted using the Properties... button, but just leave these values at unity. These are the material properties relative to vacuum. So we are setting the background material to vacuum. (Note that the properties of air are very close to vacuum.)

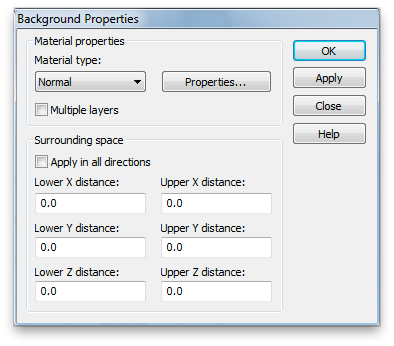
It’s a common mistake to omit this step and not realize that all the undefined regions in you simulation are the default, PEC, that is a perfect electric conductor.

Now select the Modeling tab. Use the Brick tool to create a cube of brain grey matter, 10mm on side. The tool is a small cube on the command ribbon.

Hit escape to pull up the numerical entry panel. Set the dimensions as shown and select [Load from Material Library...] from the Material: menu. Load the lossy FR-4 from the material library as shown.

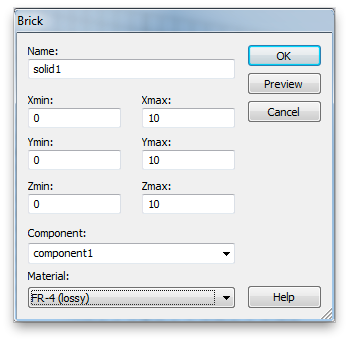
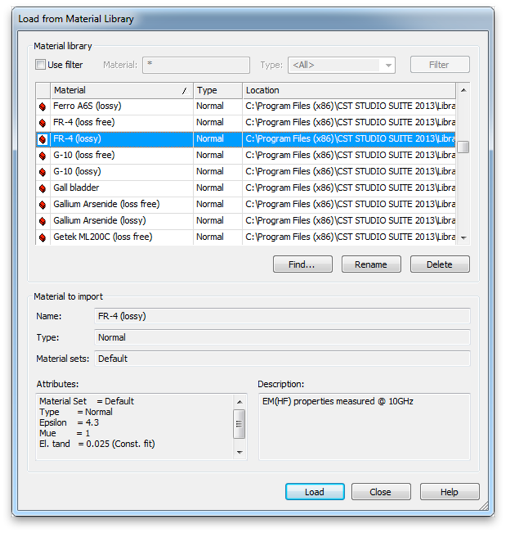
The FR-4 cube.

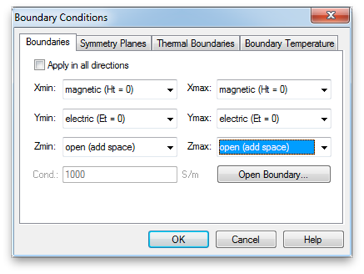
Next go back to the Simulation tab, and click Boundaries. Set the boundary conditions to magnetic (Ht=0) on the two X-planes, electric (Et=0) on the two Y-planes and open (add space) on the two Z-planes. This creates a TEM waveguide, something difficult to do in the lab, but easy in simulation.

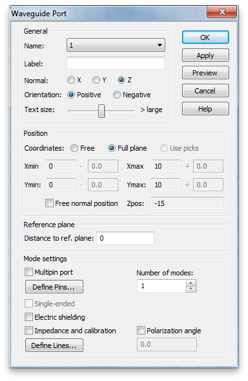
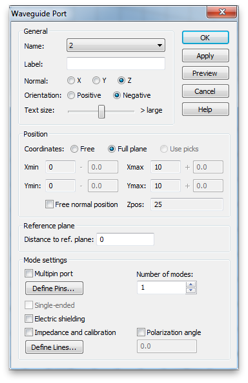
By clicking Waveguide Port, create two waveguide ports. Use all default values, except choose Negative orientation for the second one.

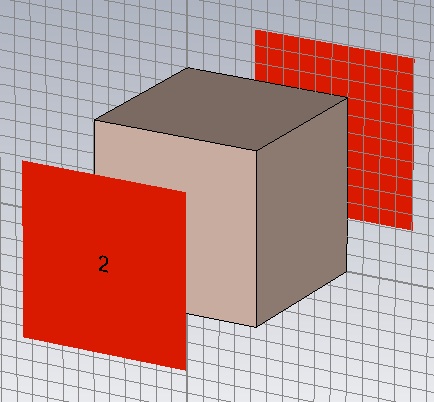
Now click Start Simulation, which will open the Time Domain Solver by default. (You can select other solvers on the Home tab.) Set the Accuracy to -50 dB, the Source Type to Port 1 and check the Adaptive mesh refinement box. Start the simulation.

Click Mesh View, so you can watch the adaptive mesh refinement as it proceeds.  As the mesh refinement proceeds, try different mesh view options to visualize the 3D structure of the mesh. Note that at the beginning of each simulation, the ports are adaptively meshed before the volume is simulated.

Port 2 mesh.

Simulation domain volumetric mesh, x-plane shown.

You can also watch the convergence by viewing: 1D Results>>Adaptive Meshing>>S-Parameters>>S21 or S11 from the Navigation Tree, on the left. The default view is the real part of the S-Parameter.

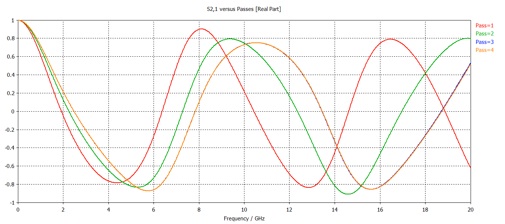
The simulation stops when the S-parameters converge. You will be asked if you want to disable further adaptive meshing. Click yes.

The S-parameters represent the amplitude and phase of the reflected and transmitted waves relative to the incident wave. The waves in question are the modes of the ports. It is very important to always look at the port modes to see if they are as you think.

From the Navigation Tree select 2D/3D Results>>Port Modes>>Port 1>>e1. (Also look at h1 as well as Port 2.)

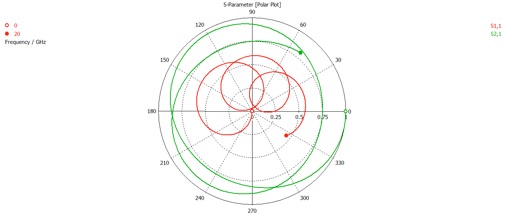
Now we want to export the magnitude and phase of just the final S-parameters (not all the adaptive passes). Click 1D Results>>S-Parameters. Then click Polar in the 1D Plot tab.

Select the Post Processing tab, and click Import/Export. Then select Plot Data (ASCII)... and save the text file to an appropriate location. The file should look like this:

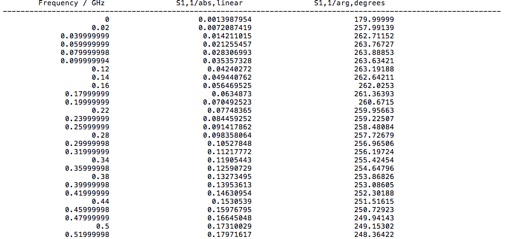
Load the data into your favorite analysis package (e.g. MATLAB or Mathematica). Plot the linear magnitude of S11 and S21 (second column of file) versus frequency (first column of file). (Note that the S11 data is at the top of the file and the S21 data begins half way down.) Make sure this plot looks like the S-parameter plot in Microwave Studio that you get when you select Linear from the 1D Plot tab.

You will also need the material properties for FR4 that were used in the simulation. In the Navigation Tree select 1D Results>>Materials>>FR-4 (lossy)>>Dispersive. Again, select the Post Processing tab, and click Import/Export. Then select Plot Data (ASCII)... and save the text file to an appropriate location.

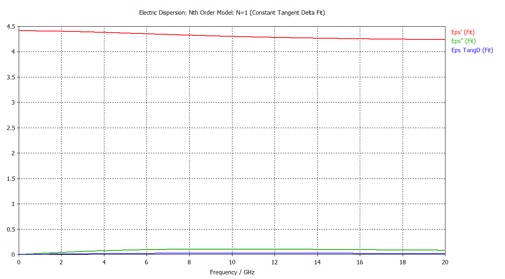
The resulting file will contain the real and imaginary parts of the FR-4 permittivity, and the their ratio, tanδ. Note, that CST uses the engineers’ convention for the time dependence of harmonic functions

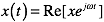
and not the physicists’ convention

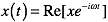
so that, for example, passive materials have a negative imaginary part. However, CST uses the primed and double primed symbols to represent the real and negative imaginary part of a complex quantity

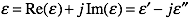
Also, tanδ is usually considered to be a positive quantity for passive materials, regardless of convention.

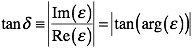
tanδ is a commonly specified material property that gives a measure of the lossiness of a material.

1. 1.Now plot the corresponding analytical result for the S-parameters using equation 1 and 2 of this article and the material properties for FR-4 that you exported from CST. For each S-parameter, put the curves for the simulation and analytical results in the same graph for comparison. Adjust the styles and/or point density so both results can be clearly seen.
   

Note that this is a physics article so that coefficients r and t’ are related to S11 and S21 through the complex conjugate

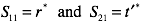
The wave vector, k, in equation 1 and 2 is the free space value and the speed of light in the units we are using is about 300.

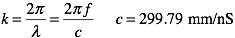
Also, d, is the thickness of the material, which is in our case 10mm. The refractive index, n, and the relative impedance, z, are related to the relative permittivity, ε, and the relative permeability, μ, in the usual way

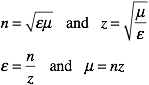
Now lets see if the simulation and analytical results agree in phase as well as magnitude.

2. What is the significance of the frequencies at which S11 is a minimum and S21 is a maximum? (Hint: consider the phase advance that a wave undergoes making a round trip inside the FR-4 slab.) Do these frequencies agree with the simple formula that describes the condition? (You can use the nominal value of 4.3 for the permittivity of the medium for calculating the wavelength or propagation constant.)

3. On one graph plot the real and imaginary parts of S11 versus frequency, both from simulation and equation 1 and 2. (Make sure you conjugate either the simulation or analytical results so that both use the same time harmonic function convention.) Make a second graph of this type for S21.

4. Explain why these results do not show agreement between simulation and analytical results.

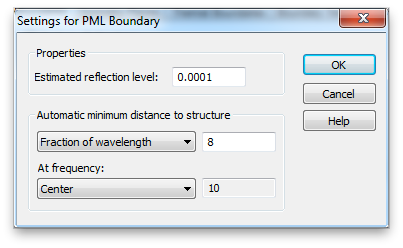
Now we will fix the problem by de-embedding the simulation S-parameters. We will accomplish this by shifting the port reference planes. The open (add space) boundary assignment has added some background media of thickness equal to one eighth of the wavelength (in the background medium) at the center frequency (10 GHz). You can check or change these settings by clicking the Open Boundary... button in the Boundary Conditions panel.

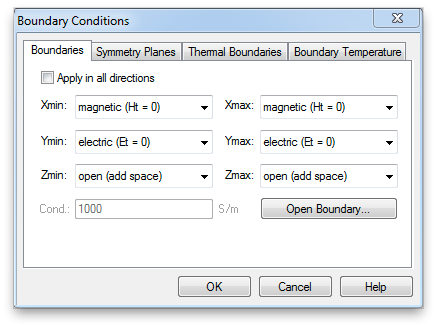
Now open the Waveguide Port panel by double clicking a port in the Navigation Tree.

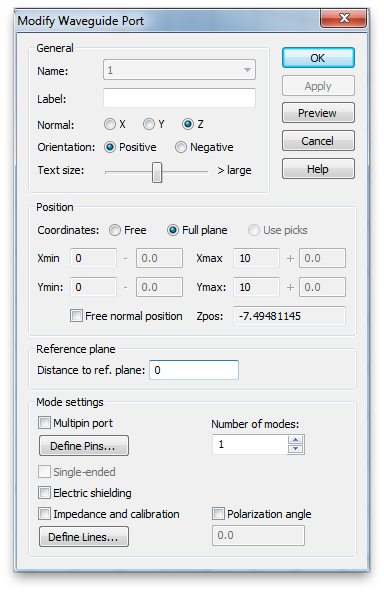
Enter the correct value in the Distance to ref. plane box. (You may enter an expression that uses arithmetic operators if you like.) A negative value moves the reference plane in toward the Teflon block. Make sure the reference plane lies on the block as shown.

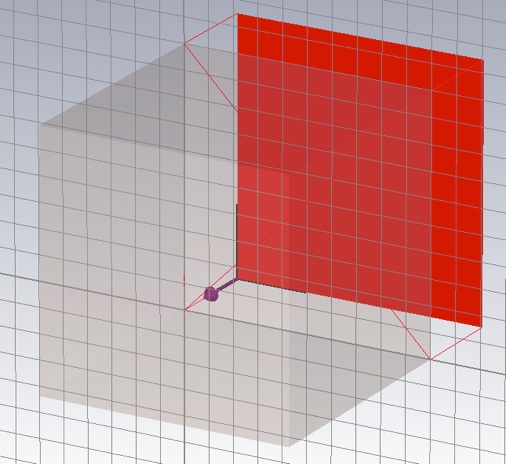
Do the same for the other port, then re-run the simulation and export the data.

5. Re-do the graphs, as in 2 above, with the new data. How is the agreement now?

6. 6.Finally calculate the fraction of the incident power that is absorbed in the FR-4 and plot it versus frequency.