Assignment

We will start by simulating a half-wave dipole antenna in the GSM1900 band. Use the following starting values for your global variables:

Operating center frequency: 1.96 GHz (middle of the GSM1900 downlink band)

Antenna end-to-end length (starting): half wavelength at the operating frequency, lambda/2

radius: 1.5 mm

gap: 3mm

Set the usual units, and set the background material to normal. Set the frequency range to include the operating frequency, maybe 0 to 3 GHz. Create two identical cylinders of lossy Aluminum along the z-axis with a gap between them. (They should be centered on the origin so you can use symmetry planes to speed up the computation.)

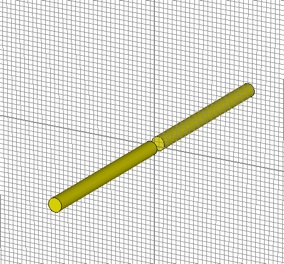
Add a discrete port that spans the gap and is parallel to the z-axis.

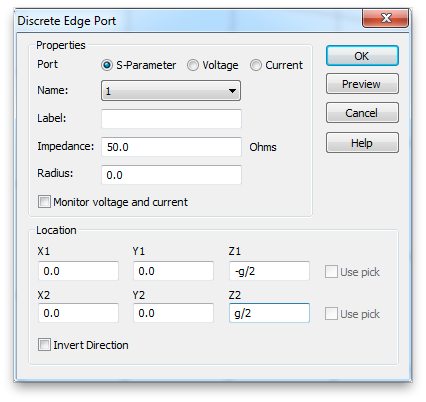
Set the global mesh properties so that there are more than two mesh intervals across the diameter of the antenna cylinders and across the feed gap.

Set all the boundary conditions to open (add space). Then select the Open Boundary  set the frequency at which the wavelength based space is calculated to our operating frequency.

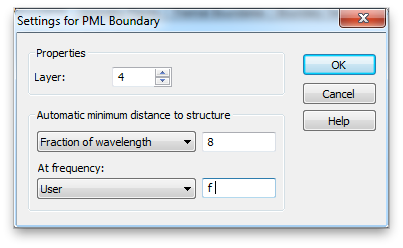
Use all three symmetry planes. Choose magnetic or electric for each symmetry plane to match the properties of the fields driven by the discrete port.

Run the simulation with an accuracy of -50dB. Is the minimum of S11 at the operating frequency? If not use the optimizer to adjust the length of the antennas so that the S11 minimum lies at the operating center frequency. You should set the range of the antenna length parameter so that it goes down to 60 mm or so. You should also reduce the the domain accuracy to find the optimal length to within 0.1 mm. (Any more precision is unnecessary and takes more simulation time.) Since there is only one dip in the S11 spectrum (for our frequency range), a local optimization algorithm is should be more efficient.

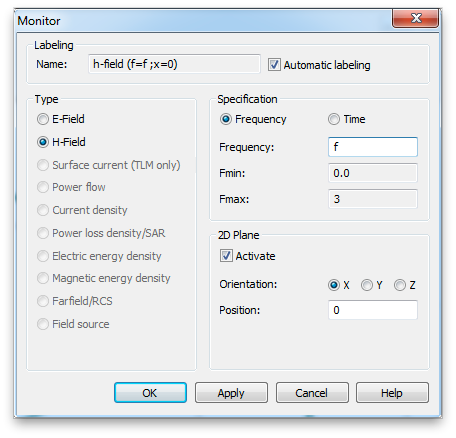
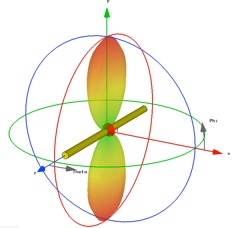
Now add a far-field monitor at the operating center frequency and re-simulate using the optimized length. Also add an H field monitor so we can verify the current distribution is in fact what we expect for a half wave dipole. Set this monitor also at the operating center frequency and activate the 2D plane (either x or y).

Run the transient solver.

1. Provide a Smith chart for S11, with the operating frequency tagged with a curve marker. Note the proximity of the impedance at the operating frequency to the port impedance.

Check that the component of field normal to the 2D plane has the expected mode shape.

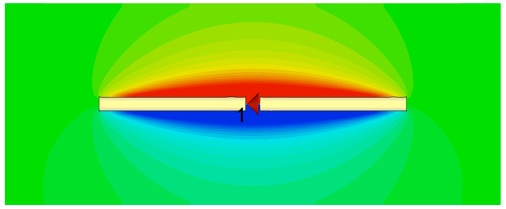
Now look at the far fields. Select Farfields>>farfield in the Navigation tree. Now select Farfield Plot Properties from the contextual menu. If you check Linear scaling in the Plot Mode tab, the plot and the numerical efficiencies will be given in linear units.

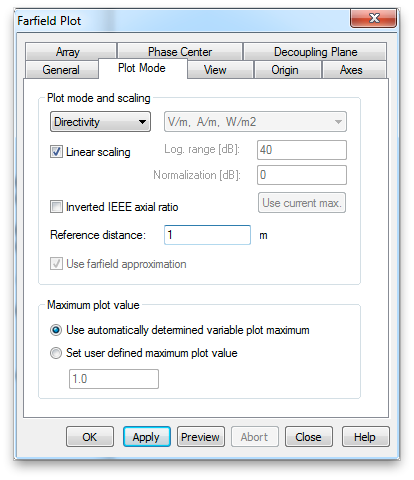
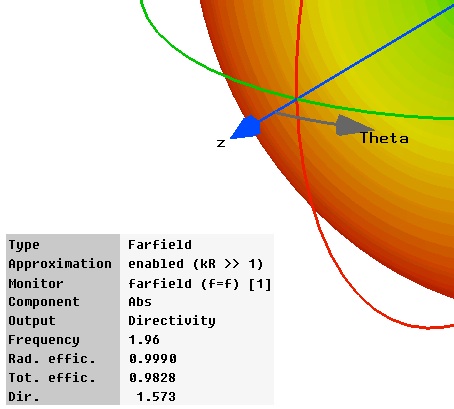
2. As in assignment 4, report the reflected, radiated and absorbed power. (In this case there is no power transmitted to another port.) Was the absorbed power less than you expected? Why do you think it is so low?

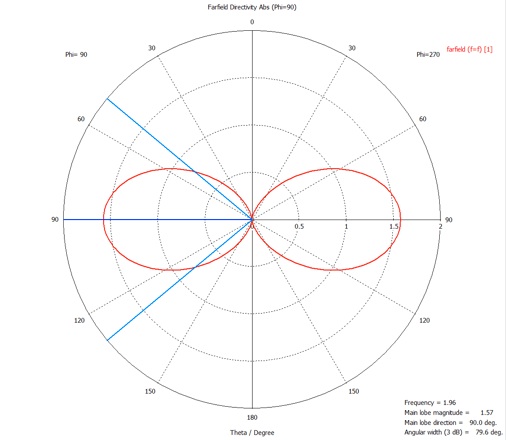
Now we want to export the directivity to compare with a theoretical dipole. Select Directivity in the Plot Mode tab and select Polar and Theta in the General tab. (Since the antenna is complete symmetric in the phi direction, so is the directivity. There is no need to look at the phi dependence.)

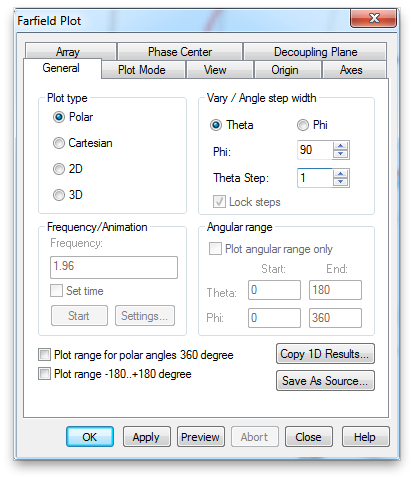
Export the data.

3. 3.Plot the directivity data in linear polar form together with the theoretical directivity of a half-wave dipole antenna. Can you suggest a reason why the directivity might differ from the theoretical result?
   

The directivity of a half-wave dipole antenna is given in section 2.2 of Stutzman and Thiele or section 4.6 of Balanis.

Use the CST array factor capability to predict the far-field for s four element array. From the farfield results, bring up the Farfield Plot panel and select the Array tab. Select Antenna array and open the properties panel. Make a four element array along the x-axis with a Spaceshift of lambda/2 (half the wavelength at the operating frequency) and a Phaseshift of zero (i.e. a broad side array).

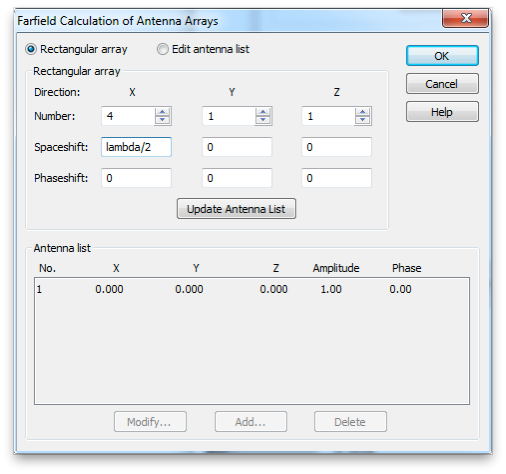
Note the drastic change in the antenna pattern.

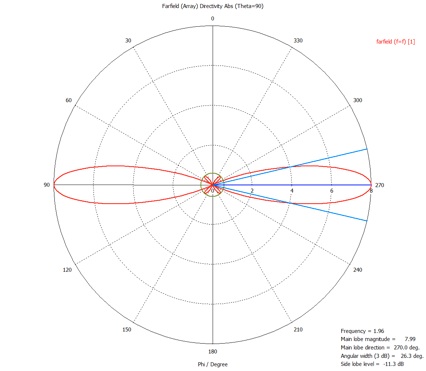
Display and export the phi dependence of the directivity with theta equal to 90 degrees.

4. 4.Plot this directivity data in linear polar form together with the theoretical directivity of the array (including both the theoretical half-wave element and the theoretical array factor.)
   

If you are having trouble doing these integrals in MATLAB, note the syntax of the following two lines of MATLAB code that compute the normalization integral for the directivity of a three element array of half-wave dipoles:

f = @(th,ph) abs(cos(cos(th)*pi/2)./sin(th)).^2.*abs(1+exp(1i*pi*sin(th).*cos(ph))+exp(1i*2*pi*sin(th).*cos(ph))).^2.*sin(th);

integral2(f,0,pi,-pi,pi)

MATLAB gives the same result as Mathematica to six decimal figures.

Now simulate the real four element array. Add three more elements to the array with positions as with the array factor above. Note that their are now two unique environments for the array elements: inner and outer. You will need to be able to tune both element types separately. Define a new length variable and use it to construct either the inner or outer elements. Also, add discrete ports for each of the new elements. (The Transform tool works on ports too.)

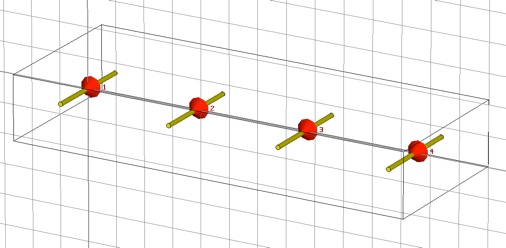
Note that one of the symmetries has been spoiled and the symmetry plane will need to be removed. In fact the simulation will not run until you do.

Run the simulation, with type of All Ports. To start with use the same length for all dipoles, the one that was optimal for the single dipole.

5. Has the S11 minimum shifted? Are the minima of S22, S33 and S44 the same as S11? Report the location (i.e. the frequency) of the minima of S11, S22, S33 and S44.

Now try to optimize the array for matched operation at our chosen frequency. We will do this by maximizing Pin1 and Pin2. (Pin3 and Pin4 have the same numerical value as Pin2 and Pin1 respectively.)

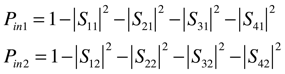
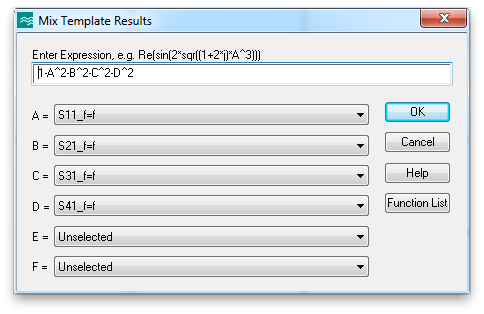
Enter all the relevant S-parameters at the operating frequency in the Template Based Postprocessing panel, and add Pin1 and Pin2 using Mix Template Results.

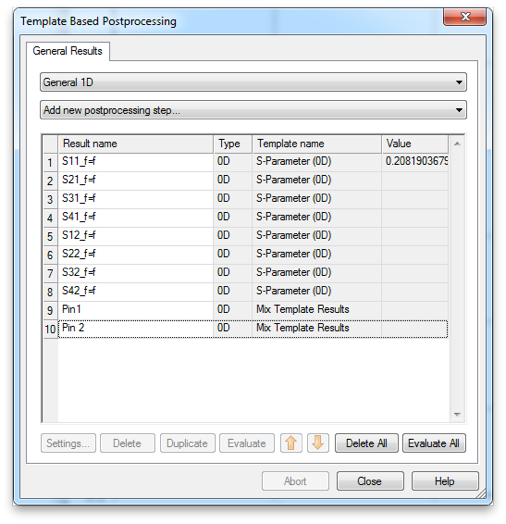
Pin1 will look like this.

Now open the optimizer and choose the antenna length parameters. You can use the same range as before.

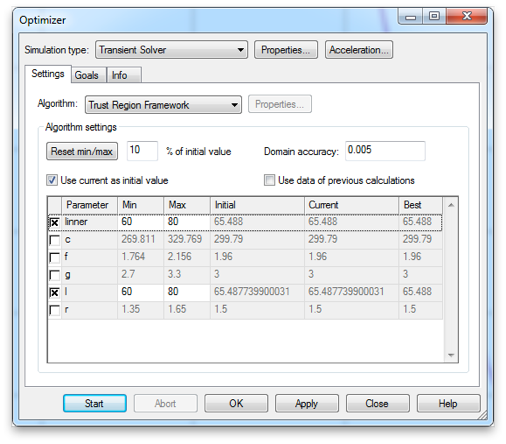
Add your 0D Pin goals. Since there are two elements of each type set the weights appropriately accordingly.

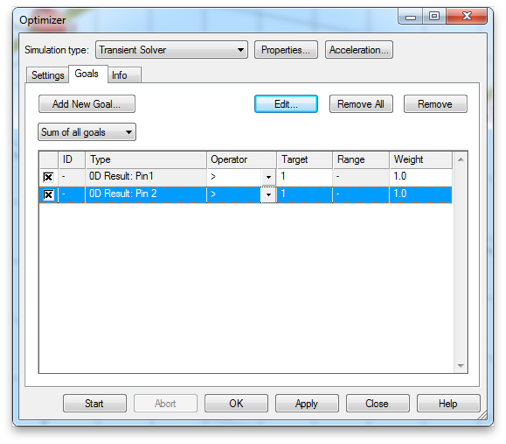
Since only S-parameters with port 1 and port 2 excited are needed for the goal function, you can speed up the optimization by using Selection for the excitation type and choosing only those ports. Now run the optimization.

6. Find the distribution of power (Prefl, Ptrans x3, Prad, Pabs) separately for each type of excitation, the outer port and and inner port.

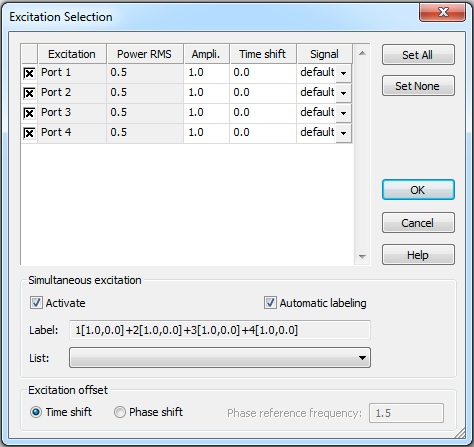
Make sure the optimal lengths are set for the all the elements and simulate with simultaneous excitation of all four of the ports. Open the Excitation List from the Transient Solver panel and check Activate in the Simultaneous excitation area. Leave the default amplitude and time shift. Since we want our array to be driven in phase, there is no time shift. Click OK an then Start.

Again plot the phi dependence of the directivity at theta equals 90 degrees, making sure the array factor is deactivated (i.e. select Single antenna). Export the data.

7. As in 3 above, plot this directivity data in linear polar form together with the theoretical directivity of the array (including both the theoretical half-wave element and the theoretical array factor.) Now that we have simulated real elements in a real array, is the agreement with theory worse than in 3, where we had a real element and an ideal array factor?