ECE 5340 Homework 1: NUMERICAL INTEGRATION
Assignment Objective
-- Program and test Trapezoidal and Simpson's integration methods
-- See effect of
• order of function
• resolution of integration (h)
-- Programming skills
• general review
1. Write a program that computes 1-dimensional numerical integration using both Trapezoidal and Simpson's methods.
Programming style: Use LOTS of comments in your code, and label every variable. Be sure every program is labeled with your name, the homework number, and the directory and filename where it can be found. Remember that you will probably need to use these subroutines later in the quarter, so write them clearly enough and general enough that you can read and use them later on!
2. Use your program to compute the definite integral
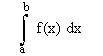 (1)
(1)
where f(x) = x
f(x) = x2
f(x) = x3
f(x) = x4
and the limits of integration are
a = 1.0
b = 2.0
Use n = 10 points in your integration, so that the size of each division, h = (b – a)/n = (2.0 – 1.0)/10.
3. Calculate the expected values of the integrals, and the expected value of error for each method. Compare the results by filling in the tables on pages 3-4.
![]()
![]()
Observed Error = Calculated Value – Analytical Value
4. Now let n = 20, and recalculate errors for the case of f(x) = x4.
5. Add another subroutine to your program to compute
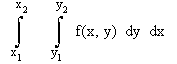 (2)
(2)
You may use either Trapezoidal or Simpson's integration. Use your program to calculate the integral in (2) for
a. f(x, y) = xy
b. f(x, y) = x4y4
c. f(x, y) = exy Analytical (Maple) = 8.258
with x1 = y1 = 0 x2 = 1 y2 = 3
6. Summarize your results and comment on any unexpected result. Your summary should state the effect of the order of the function, the resolution of the integration, and the use of double precision.
7. Optional 5% extra credit
Experiment with the Numerical Integration function in Matlab, or another software package that you routinely use. Examine how it handles high order functions, and determine if and when it could make mistakes.
Name ____________________________________ ECE 5340 Homework No. 1
NUMERICAL INTEGRATION
Your grade: Calculations are correct __________/15
Program works correctly __________/60
Program style __________/25
Total __________/100
Table 1. Values of the integral given in (1). (n = 10)
|
f(x) |
Analytical Value |
Trapezoidal Value |
Simpson's Value |
|
x |
|
|
|
|
x2 |
|
|
|
|
x3 |
|
|
|
|
x4 |
|
|
|
Table 2. Error of the numerical calculation of the integral in (1). (n = 10)
|
f(x) |
Expected Value of Trapezoidal |
Observed Value of Trapezoidal |
Expected Value of Simpson's |
Observed Value of Simpson's |
|
x |
|
|
|
|
|
x2 |
|
|
|
|
|
x3 |
|
|
|
|
|
x4 |
|
|
|
|
Table 3. Error of the numerical calculation of the integral in (1). (n = 20)
|
f(x) |
Expected Value of Trapezoidal |
Observed Value of Trapezoidal |
Expected Value of Simpson's |
Observed Value of Simpson's |
|
x4 |
|
|
|
|
Table 4. Values of the integral given in (2).
|
f(x) |
Analytical Value |
Calculated Value |
|
xy |
|
|
|
x4y4 |
|
|
|
exy |
8.258 |
|
[ ] Source code listing attached (hard copy)
[ ] Calculations of expected values of integrals attached
[ ] Calculations of expected values of error attached
[ ] SUMMARIZE your results and COMMENT on any unexpected results.
Grade = ________ / 100
Any Comments from the Grader:
Your Random Student # that will be used for
posting grades on the website is ___________.
HOMEWORK NO. 1
How many hours did this take? ___________
How much did it help you learn about numerical integration?
little some a lot
How difficult was it to program?
hard medium easy
COMMENTS: