ECE 5340/6340 SOR: Successive Over-Relaxation Method

---

ITERATIVE METHODS OF SOLVING MATRIX EQUATIONS:

Particularly good for solving sparse matrix equations (Finite Element method and Finite Difference Method)

Solve A x = b

Back Substitution Algorithm:

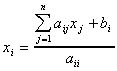For i=1,2,3,…n

In regular back substitution, we know x_j. But what if we didn't? We could guess! These iterative methods are based on how to choose and improve that guess.

---

Jacobi's method

Initial guess: x⁽⁰⁾ = 0

Then at each (k^th) iteration find the next (k+1)^th values of x:

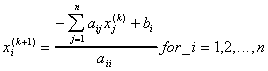
For a banded matrix, this summation can be limited to the bands

For the Jacobi method, new (k+1) values are not used until the next iteration.

---

Gauss-Seidel

This method improves on the Jacobi method by using new values that have been obtained prior to each step in the iteration. This gives faster convergence.

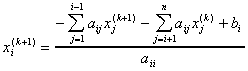
New values are used as soon as they are generated.

---

SOR: Successive Over-Relaxation

Relaxation moves towards solution faster:

From Gauss-Seidel:

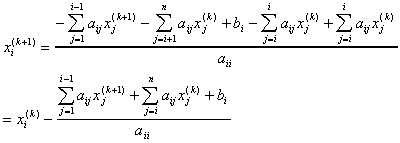
This can be written:

Where R_i is the "Residual" (error or change)

Now, use relaxation (w ) to speed convergence:

How to choose w :

1. For w =1, this reduces to Gauss-Seidel
2. Method converges when 0<w <2 for a positive-definite matrix. (When matrix is reduced to diagonal, all elements are positive.)
3. 0<w <1 Under-relaxation slows convergence
4. 1<w <2 Over-relaxation speeds convergence
5. w optimal is based on spectral radius, which is difficult (expensive) to calculate.
6. For square matrices, w optimal can be approximated:

w = 4 / (2+Ö ( 4 + C*C) )

C = cos (p / p) + cos(p / q)

p,q = # of mesh divisions on x,y sides

---

EXAMPLE:

See web