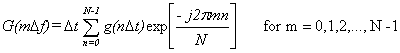Faster than Fourier –

Ultra-Efficient Time-to-Frequency Domain Conversions for FDTD Simulations

Cynthia M. Furse, Department of Electrical and Computer Engineering

Utah State University, Logan, Utah 84322-4120

E-mail: furse@alpha.ece.usu.edu

Phone: (435) 797-2870, Fax: (435) 797-3054

Keywords: FDTD methods, Computation time, Frequency domain analysis, Time domain analysis, Discrete Fourier transforms

Abstract

This tutorial compares several methods of converting from the time-to-frequency domain for FDTD simulations. Applications include calculation of field or power distribution, antenna impedance and radiation pattern. The traditional fourier transform methods are compared to two methods based on the solution of linear equations. This tutorial describes how to program and use these techniques, and evaluates their effectiveness for several applications including analysis of a millimeter-resolution human model underneath a 60-Hz power line, antenna radiation pattern and impedance calculations, calculation of coupling of a cellular telephone to the human head, and geophysical prospecting simulations.

1. Introduction

Many applications of the finite-difference time-domain (FDTD) method require conversion of time-domain field data to frequency domain data (magnitude and phase) over large regions of the model. Applications include bioelectromagnetic dosimetry calculations of the human body for analysis of cellular telephones [1-4], power lines [5,6], and other EM-safety studies [7], antenna impedance and radiation patterns [8], radar cross section calculations [9], and calculations of S-parameters of microwave circuits [10]. Time-to-frequency domain conversions have traditionally been done with either the fast fourier transform (FFT) [11-12] or the discrete fourier transform (DFT) [13-14]. When multiple frequencies are of interest, the FDTD method is commonly used with a pulsed excitation, and the fourier transform methods are used to obtain the desired results at these frequencies. More recently, methods based on the solution of linear equations have been found to be more efficient than the fourier transform methods [15].

This tutorial compares the traditional fourier transform methods and methods based on solution of linear equations for time-to-frequency domain conversions for FDTD simulations. Equations are given for computing memory and computational requirements for individual applications. In addition, the use of these methods for specific electromagnetic applications is discussed.

A brief outline of the computational aspects of the FDTD method is given in Section II. Section III briefly describes the fourier transform methods and their computational requirements. It also describes methods that have been used to optimize the fourier methods. Section IV describes two methods based on linear equations that can be used in place of fourier transform methods. The first of these methods is the two-equations two-unknowns (2E2U) method that can be used for single-frequency FDTD simulations. The second of these methods is its extension to multiple frequencies, called the N-equations and N-unknowns (NENU) method. Section V gives examples of the types of calculations that are needed in realistic applications and compares the computational requirements and relative advantages of each of the methods, with the hopes of providing the user with guidance for choosing the optimal method for a specific application.

II. Computational Aspects of the FDTD Algorithm

The FDTD algorithm has been described in detail in available literature, [16,17] so it will not be described here. The general forms of the FDTD equations for the three electric field components (E_x, E_y, E_z) and three magnetic field components (H_x, H_y, H_z,) are shown below:

E_x(i,j,k) = E_x(i,j,k) + C₁ (H_z(i,j,k) – H_z(i,j-1,k) + H_y(i,j,k-1) – H_y(i,j,k)) (1)

H_x(i,j,k) = C₂ H_x(i,j,k) + C₃ (E_z (i,j,k) – E_z(i,j+1,k) + E_y(i,j,k+1) - E_y(i,j,k))

where the constants C₁, C₂, and C₃ depend on the electrical properties of the material at each point (i,j,k) in the model. The number of real multiplications required for computing this algorithm per time step are:

Number of multiplications = 9 N_xyz

where

N_xyz is the number of FDTD cells = N_xN_yN_z

For the purposes of this tutorial, additional computational overhead for initialization of the simulation, boundary conditions, and incidental calculations will be neglected. In practice, it is common for boundary conditions to take 10 to 30% of the total computational time, depending on the simulation size and boundary conditions used, so these computational costs are not necessarily negligible in practice. They are neglected here because they have no effect on or from the time-to-frequency domain conversions, which is the topic of this paper.

The storage requirements for the FDTD simulation (again neglecting boundary conditions and incidental storage) is one real value for each of the six vector field components and one for an integer indicating what dielectric material exists at each FDTD cell location:

RAM required for FDTD = 7 N_xyz

Disk required for FDTD = 0.

These values are shown in Table 1, which is used throughout this tutorial to

summarize computational requirements.

III. Fourier Transform Methods (DFT or FFT)

Fourier transform methods are the traditional methods of converting from the time to frequency domains for most discrete applications including FDTD. They are very accurate, can be used with either single or multiple frequency simulations, and there are numerous commercial software packages available for making these calculations.

The discrete fourier transform (DFT) [18] is based on a running summation of the time domain field as given below:

1(2)

where

G(mDf) = the complex value of the magnitude and phase of the equivalent steady-state sine wave at frequency mDf

g(nDt) = the time-domain value of the pulse at time nDt

N = length of the fourier transform = 1/ (Df Dt)

Df = the frequency resolution of the frequency-domain calculations

m = the frequency index, m=0,1,2,...,N-1

Dt = the sampling period of the DFT

Normalization is normally required in order to obtain frequency domain data equivalent to the magnitude and phase of a 1 V/m incident sine wave at each frequency of interest. Since commonly-used pulse shapes do not have constant frequency responses, the final values must also be normalized by (divided by) the complex DFT of the incident pulse. This normalization step can be eliminated by used a step-function which has a constant (unity) frequency spectrum [15,33]. Numerical dispersion in the FDTD grid eliminates the high frequencies, so they do not cause aliasing errors or otherwise interfere with the solution. Since the normalization requires only a single fourier transform which is reused for all points in the grid, the choice of pulse shape and the issue of normalization has negligible effect on the computational requirements of the simulation.

The computational requirements of the DFT are:

Number of (complex) multiplications = N_FDTDN_PxyzN_PN_F

where

N_FDTD = Number of time steps in the FDTD simulation

N_F = Number of frequencies of interest (number of DFT summations)

N_P = Number of Parameters of Interest (six vector field components, for instance)

N_Pxyz = Number of points of interest (such as all locations within the grid, for complete field distributions, a set of surfaces for radiation pattern, or a few isolated points for impedance calculations)

The storage requirements of the DFT are:

RAM required for DFT = 2N_PxyzN_PN_F

Disk required for DFT = 0.

This assumes that the DFT summation is computed as a running sum inside the FDTD code, rather than storing all of the time domain values for later processing with commercial software. In practice, disk storage and later computation with commercial software is only possible when a very limited number of time-to-frequency conversions are of interest (such as impedance calculations). For problems requiring fourier transforms for surfaces or volumes of points, the storage requirements (either RAM or disk) become prohibitively large.

The fast fourier transform (FFT) was developed as an efficient method of computing the fourier transform.[18] The complete time history of the values at all points of interest is stored, and the exponential components are computed iteratively. In the Radix-2 algorithm, a commonly-used algorithm because of its high efficiency, the length (N) of the fourier transform is 2ⁿ. Most FDTD simulations are run for some arbitrary number of time steps, not necessarily 2ⁿ. This is not a problem however, as the FDTD pulsed data can be padded with zeros to create an array with length suitable for the Radix-2 algorithm. However, even with the use of the Radix-2 algorithm, the FFT has been shown to be computationally more expensive than the DFT for all FDTD simulations. [19]

One of the limitations of the traditional FFT has been that it requires evenly-spaced data (not suitable for exponentially increasing time steps), and that it produces evenly-spaced frequency data (difficult to obtain exactly the frequencies of interest). This limitation has been partially solved by the use of the unequal-spaced FFT. [20] The storage and computational requirements are similar, however, so this method is not useful for FDTD simulations requiring a large number of time-to-frequency domain calculations.

Desampling has been used to minimize the computational requirements of fourier transform computations.[14] This minimizes the number of FDTD samples used to obtain the fourier transform. Since FDTD calculations are oversampled according to the Nyquist criterion [14,19], not all of them are required for fourier transform calculations. If, for instance, only every tenth FDTD sample is chosen for computation of the fourier transform, the computational requirements of the fourier transform are divided by ten. This method still relies on the samples being evenly spaced, and requires storage of the running sum, so the memory requirements are the same as for the DFT. Desampling rarely improves the efficiency of the fourier transform by more than a factor of 10.

Fourier transform methods are limited for use in low frequency high resolution simulations (such as analysis of a millimeter resolution model of the human body under a 60 Hz power line), where the sampling resolution of the wave form is ultra high. For single-frequency (CW) simulations, the fourier transform calculations must be made over a full half-cycle of the converged sine wave. This requires at least an additional half-cycle of FDTD calculations, which can be difficult or impossible for low frequency calculations, and which increases the cumulative error inherent in the finite-difference calculations.

The computational cost of the Radix-2 FFT scheme is typically:

Number of (complex) multiplications = (N_FDTD/2)log₂(N_FDTD N_PxyzN_P)

The storage requirements of the FFT are:

RAM required for FFT = 2N_PxyzN_PN_F

Disk required for FFT = N_FDTD N_PxyzN_P

IV. Linear Equation Methods

As an alternative to fourier transform methods, this paper presents two methods that overcome many of their limitations and have the added advantages of flexibility and programming simplicity. Both methods are based on the solution of linear equations. The first method, called the two-equation two-unknowns (2E2U) method, for use with single-frequency analysis is significantly more efficient than fourier transform methods and can be applied effectively for an extremely broad frequency range from the low kHz to high GHz and beyond. This method has the added advantage that for many applications, it can be applied with virtually no memory or computational requirement (beyond the FDTD requirements themselves). [15]

The second method, called the N-equation N-unknown (NENU) method, is an extension of the first method and can be used for multi-frequency analysis. In theory, this method minimizes computational and memory requirements for any simulation. However, computer round-off errors limit its application somewhat. Trade-off curves are presented that show that this multi-frequency extension is the most efficient method for up to about 40 frequencies, and that the single-frequency method is preferable for larger numbers of frequencies. [21]

These two methods are presented below.

a. Two Equations - Two Unknowns Method

The two-equations two-unknowns (2E2U) method is a simple, direct method to obtain the magnitude and phase of a sine wave in the time-domain based on writing two equations in two unknowns (magnitude and phase) for the time-domain fields, and then solving them directly for the magnitude and phase. At a given location in space, we can write

A sin (wt₁ + q) = q₁

A sin (wt₂ + q) = q₂ ⁽²⁾

where A is the magnitude, q is the phase angle, and w ( = 2 p F) is the angular frequency. At two time steps, t₁ and t₂, the values q₁ and q₂ are obtained from the FDTD simulation. These equations can be solved for the unknowns, A and q, to give direct relationships for these values:

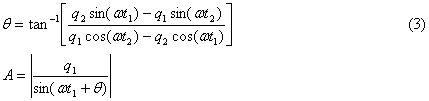
The choice of t₁ and t₂ depends on the simulation. For most FDTD simulations the spatial resolution Dx is on the order of l / 10 to l / 100. For these simulations t₁ and t₂ can be the last two time steps of the simulation. For higher-resolution simulations the time resolution is also high (Dt = Dx/2c), so q₁ and q₂ are nearly equal if t₁ and t₂ are very close. This results in errors due to numerical round-off when calculating A and q. For these simulations, it is better to choose t₁ to be a few time steps (say, 50) before the end of the simulation, and t₂ to be the final time step such as was done in [6].

The equations in (3) can be programmed one of two ways, depending on t₁ and t₂. The first is to store (or output to disk) the value of q₁ at time step t₁, and then when the final time step, t₂, is reached, the values of A and q can be calculated. This is necessary if t₁ and t₂ are not subsequent time steps. An alternate method of eliminating the memory requirement can be used when t₁ and t₂ are taken to be the last two time steps. For the final time step, q₁ is stored in a single location (not an array), then q₂ is calculated from the last time step of the FDTD algorithm. This gives A and q which can be output to disk or stored in the same locations as the fields used to compute them (remember FDTD is now finished). This is then repeated for each location.

The 2E2U method provides accurate magnitude and phase calculations for simulations with clean, sine wave output. Noise and DC offsets will cause errors. Ramped sine excitations known not to cause a DC offset should be used [22] or a pulse with a very smooth turn-on [23]. Ramped sine excitations have also been observed to reduce or eliminate numerical noise in FDTD simulations [24].

The computational requirements for this method are :

Number of multiplications = 4N_PN_Pxyz

The memory requirements for this method are:

RAM required for 2E2U (storing t₁ timestep) = N_PN_Pxyz

RAM required for 2E2U (using last timesteps) = 0

Disk required for 2E2U = 0

b. N-Equations N-Unknowns

The two-equations two-unknowns method can be extended to multiple frequencies. In this case, N-equations are solved for N-unknowns (NENU) which are the amplitude and phase at each frequency of interest. This requires samples at 2N time steps and results in the following equations for two frequencies:

A₁ sin (w₁t₁ + q₁) + A₂ sin (w₂t₁ + q₂) = q₁

A₁ sin (w₁t₂ + q₁) + A₂ sin (w₂t₂ + q₂) = q₂ (4)

A₁ sin (w₁t₃ + q₁) + A₂ sin (w₂t₃ + q₂) = q₃

A₁ sin (w₁t₄ + q₁) + A₂ sin (w₂t₄ + q₂) = q₄

This can be extended to multiple frequencies where the source is a sum of sine waves:

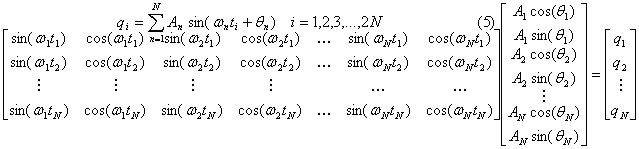
Using trigonometric identities on the sine function, this can be broken into a matrix equation which can be solved for functions (A_ncos(q_n) ) of A_n and q_n .

A standard matrix solution method such as Gaussian elimination is used to obtain the vector of functions A_n sin or cos(q_n). The unknowns A_n and q_n are then found from these functions.

This form of the NENU method requires a multi-frequency source in the form of (5), which does not utilize methods such as sine wave ramping to prevent high frequency transients or DC offsets. These specialized ramps could be included in the source type, and the same solution method could be followed by changing the specifics of the matrix above.

In theory, the NENU method provides an exact conversion from time to frequency domain. In practice, however, the matrix can be ill-conditioned because of computer round off error. This happens when the cosine and sine samples become very close together so that they are numerically indistinguishable when the time samples (t₁, t₂, t₃, etc.) are too close together, when a very large number of frequencies are involved, or when the frequencies are too close together. There is a also a problem when their relative magnitudes of the source are several orders of magnitude different (which can be prevented simply by scaling magnitudes AFTER time-do-frequency domain calculations). This paper discusses each of these problems and the efficiency tradeoffs for solving them.

As an example of the application of the NENU method solutions were computed for twenty-five different frequencies as a function of the spacing of the time samples (t₂ = t₁ + nDt). The frequencies are evenly-spaced from 0.1 to 1 MHz, and have equal magnitudes. The time resolution Dt = Dx / 2c, where Dx is the spatial resolution of the FDTD grid, and Dx = l_min / 20. Figure 1 shows the inverse of the condition number. A large condition number (small inverse) indicates a poorly-conditioned matrix. The spikes seen in the inverse condition number indicate sample spacings providing most accurate matrix solutions. These are clearly sporadic. In particular, note that simply taking time samples that are far apart does not ensure accurate matrix solution. Figure 2a shows the maximum error in the computation of amplitude when using the simple Ax=b form and Gaussian elimination as a function of sample spacing. Errors of less than 1% are obtained when samples are spaced at least seven samples apart, and low errors are obtained for all of the sample spacings that provide high inverse condition numbers in Figure 1. A difficulty with using sample spacings that are far apart is that additional FDTD time steps must be run beyond convergence of the solution. Improvements can be made. The singular value decomposition (SVD) is commonly used to solve ill-conditioned matrices by removing or reducing the near-zero eigenvalues. Figure 2b shows the maximum error in the computation of the magnitude using the Singular Value Decomposition and related psuedo-inverse to solve the matrix equation. Using SVD provides accurate calculations (less than 1% error) for all time sample spacing. This enables calculations of magnitude and phase of twenty-five frequencies using the last fifty converged time steps of the FDTD simulation.

The accuracy advantage of using the SVD becomes more pronounced as the number of frequencies increases. For instance, it was found that for 100 frequencies evenly-spaced from 0.1 to 1MHz, the SVD can provide calculations with less than 1% error for sample spacings greater than four, whereas the direct method without SVD requires at least a spacing of twenty-one samples.

The computational requirements for the N-equation N-unknown method using Gaussian elimination are [25] :

Number of multiplications = 9N_DFDTDN_xyz + N_PxyzN_P (2N_F )³ /3

The computational requirements for the N-equation N-unknown method using SVD are [26] :

Number of multiplications = 9N_DFDTDN_xyz + 12N_PxyzN_PN_F³

The memory requirements for NENU are:

RAM required for NENU = (2 N_F)² N_Pxyz N_P

Disk required for NENU = 0

It is clear that there is a substantial tradeoff between accuracy and efficiency in the NENU method using Gaussian elimination or SVD. This will be examined for specific applications below.

V. Applications

This section outlines several applications of time-to-frequency domain calculations and the computational aspects surrounding them. Four specific applications will be considered. These are computation of (a) antenna impedance, (b) radiation pattern, (c) absorbed power or field distributions such as for cellular telephone analysis, and (d) low frequency high resolution simulations such as analysis of a millimeter resolution model of the human body in the presence of a 60 Hz field.

The computational requirements for the different methods of converting from time to frequency domains are compared in Table 1. Their relative efficiency depends on the number of frequencies of interest and the number of parameters and locations where the conversions must be made. This is application dependent. Figure 3 shows the effect of frequency for an application where a large number of time-to-frequency domain conversions are required (such as analysis of cellular telephones). For a small number of frequencies (1 or 2), the 2E2U method is the most efficient. For a larger number of frequencies (up to about 37) the NENU method using gaussian elimination is most efficient. For more frequencies than that, the DFT is more efficient because it does not require additional FDTD time steps. This figure also emphasizes the importance of choosing the most efficient method for the application, because of the extremely large computational burden of computing magnitude and phase as compared to simply running the FDTD simulation.

The relative efficiency of the methods depends strongly on the application. Table 2 summarizes the computation and memory requirements of the various methods for the applications discussed below.

a. Impedance Calculations

Impedance calculations require relatively few time-to-frequency domain calculations. Impedance is generally computed as Z = V / I , where Z,V,I are complex values. The voltage is found from the line integral of the electric field (requiring one electric field component), and the current is found from the closed contour integral of the magnetic field (requiring four magnetic field components) around the electric field that is used to find the voltage [1,8]. Thus, only five time-to-frequency domain conversion may be required to compute impedance. Table 2 shows the relative computation and memory requirements for an example that has the following parameters:

Number of Frequencies N_F = 1 and 25

Number of Parameters N_P = 5

Number of FDTD cells N_xyz = 100 x 100 x 100

Number of FDTD time steps N_FDTD = 2000 (typical for low-Q simulations)

From Table 2, it is clear that the 2E2U and NENU methods are more efficient than the DFT for single frequency calculations. For multiple frequencies, the DFT or NENU should be used, as the expense of additional FDTD simulations would negate the efficiency of the 2E2U method. For an application such as impedance calculations where few field components require time-to-frequency domain conversions, all of the methods are relatively inexpensive compared to the FDTD simulation itself. Storage is minimal for all of these methods for this application. Even the FFT with commercial software could be used for this application.

b. Radiation Pattern Calculations

Calculation of antenna radiation patterns requires a moderate number of time-to-frequency domain conversions. Equivalent surface currents are found by integrating the electric and magnetic fields tangential to a cubical surface surrounding the radiator and transformed to the far-field in either the time or frequency domains [16]. If they are converted to the frequency domain and then transformed to the far field (following the method of Van Bladel [8,27]), four tangential electric and magnetic field components are required on each of six surfaces surrounding the antenna. For an example where the total FDTD space is 100 x 100 x 100 cells, the radiation pattern may be taken five cells inside the boundary, so each of the six surfaces is 90 x 90 cells. This gives the number of parameters NP = (4 field components) (6 surfaces) (90 x 90 cells) = 194 400. Table 2 shows the relative computational requirements for this example:

Number of frequencies N_F = 1 and 25

Number of Parameters N_P = 194 400

Number of FDTD cells N_xyz = 100x100x100

Number of time steps N_FDTD = 2000 (typical low-Q example)

For this example, which has a moderate number of time-to-frequency domain conversions (two dimensional surfaces rather than three dimensional volumes), the 2E2U method would again be most efficient for single frequency calculations. NENU and DFT would be most efficient for multiple frequency calculations. The 2E2U and NENU methods would require less storage than the DFT method, although this storage is still small compared with the overall FDTD simulation requirements.

c. Field or Power Distribution

Field, power or current density distributions are commonly calculated with the FDTD method for analysis of safety guidelines or for showing color plots of these distributions. Commonly they are done for every point in a three-dimensional grid and therefore require a very large number of time-to-frequency domain conversions. Examples include bioelectromagnetics and medical imaging and inversion problems, [1-4,28] and geophysical applications [29]. In order to find the complete electric field distribution, for instance, this would require time-to-frequency domain conversions for three field components for every cell in the simulation. The relative computational requirements of the various methods are given in Table 5 using the values given below:

Number of Frequencies N_F = 1 and 25

Number of Parameters N_P = (3 fields) (Nxyz cells) = 3 000 000

Number of FDTD cells N_xyz = 100 x 100 x 100 = 1 000 000

Number of FDTD time steps N_FDTD = 2000

From Table 2, the significance of the savings that can be obtained using the 2E2U or NENU methods becomes more apparent for this application. The DFT requires about as much computational time and as much storage as the FDTD simulation itself. This means that half of the system resources are being dedicated to the time-to-frequency domain transformation. The 2E2U method provides a significant improvement for single-frequency simulations, five orders or magnitude less computation and virtually no storage requirement. This frees up system resources for larger problem sizes rather than larger post-processing applications. The NENU method is slightly more efficient than the DFT for multiple frequency simulations up to about 35 frequencies. This is an approximation and would need to be analyzed for the specific array of frequencies of interest.

In a problem of this size, the 2E2U method would not necessarily be the most efficient method, however it has potential application because of its ability to compute the frequency domain fields with virtually no memory. Many realistic simulations are constrained more by memory than computer time.

d. Low Frequency High Resolution Simulations

Low frequency high resolution simulations present a peculiar problem for time-to-frequency domain conversions that is solved using the 2E2U method. Until recently, the FDTD method was limited to applications where the simulation could be completed for at least one half cycle of the lowest frequency in the wave. This precluded low frequency analysis of high resolution models. For instance, analyzing a 6mm resolution model of the human body at 60 Hz would require 1.7 x 10⁹ time steps per cycle of the wave [6]. The use of pulsed FDTD with the fourier transform and frequency scaling [5,30] and the 2E2U method [6,31,32] have extended the range of this method to very low frequencies (down to 60 Hz). Both of these methods take advantage of the fact that the FDTD simulation actually converges in a moderate number of time steps (say 2000), and that the only difficulty is obtaining the magnitude and phase data from far less than a single cycle of the fields. This is done using the 2E2U method, and is shown to be highly accurate when compared to analytical and measured data. [6,31,32] . This has allowed direct calculation of the magnitude of 60 Hz fields within the human body with modeled resolution of 2mm. Other methods simply could not solve this problem, so the 2E2U method has been critical to the understanding of these low frequency fields.

Figure 4 shows the application of the 2E2U method to geophysical simulations.[32] This simulation analyzes a typical nickel sulfide deposit in the Kambalda formation in Australia. A perfectly conducting nickel oxide slab (shown as the vertical red line) is illuminated by a small loop at 2 MHz (star-shaped element in upper left). The resolution of the simulation is 0.5 meter, and results were analyzed at 300 and 500 kHz as well as 2 MHz. The simulation converged in approximately 1000 time steps, and a half cycle of the wave was 2000 time steps at 300 kHz. Thus, the 2E2U method was used to obtain converged frequency domain values without running a half cycle of the wave in the simulation. Values are expressed in decibels relative to the maximum value. The minimum has been clipped at –500 dB.

c. Conclusions and Summary

Figure 3 shows the relative cost of the fourier transform, 2E2U and NENU methods for an application requiring a large number of time-to-frequency domain conversions. For a single frequency, the 2E2U method is most efficient. For up to about 40 frequencies, the NENU method is most efficient.

Memory is also a tradeoff for these methods. As noted in Table 1, the DFT must store a complex value (equal to two real values) for every location and parameter of interest. The 2E2U can completely eliminate this requirement if the sampling resolution is sufficient to allow computation of magnitude and phase from the final two time steps of the simulation. The NENU method must store the matrix that is (2 NF)² where NF is the number of frequencies for each location and parameter of interest. These values would generally be written to disk, with final solution being done as a post-processing step, but this may be prohibitively expensive for some applications. The optimal method to use depends on the size of the problem and number of time-to-frequency domain conversions required.

For applications with relatively few time-to-frequency domain conversions such as antenna impedance calculations, all methods could be used. The 2E2U and NENU methods would be the most efficient. For applications with a moderate number of time-to-frequency domain conversions such as antenna radiation pattern calculations, the 2E2U method would be most efficient for single frequency studies, and the DFT or NENU methods would be most efficient for multiple frequency studies. For applications with a large number of time-to-frequency domain conversions such as computation of complete field or power distributions, efficiency of the methods is critical. The 2E2U method is clearly the most effective for single frequency calculations, and the NENU method and DFT would be used for multiple frequency simulations, depending on the number of frequencies being considered. The 2E2U method is also critical for use in FDTD simulations that are low frequency and high resolution (ultra-high resolution with respect to wavelength.

The time-to-frequency domain conversion methods described in this paper give a good range of options to choose from for different applications of FDTD simulations. Choosing the optimal method can lead to huge advantages of code efficiency and an increase in the overall problem size that can be simulated with given computer resources. The DFT, 2E2U, and NENU methods are all good choices for FDTD time-to-frequency domain conversions.

References

[1] O. P. Gandhi, G. Lazzi, and C. M. Furse, "Electromagnetic Absorption in the Human Head and Neck for Mobile Telephones at 835 and 1900 MHz," IEEE Transactions on Microwave Theory and Techniques, Vol. 44, October 1996, pp. 1884-1897

[2] M. Okoniewski, M.A. Stuchly, "A Study of the Handset Antenna and Human Body Interaction," IEEE Transactions on Microwave Theory and Techniques, Vol. 44, October 1996, pp. 1855-1864

[3] M. A. Jensen and Y. Rahmat-Samii, "EM Interaction of Handset Antennas and a Human in Personal Communication," Proc. IEEE, Vol. 83, pp. 7-17, 1995.

[4] P. J. Dimbylow and S. M. Mann, "SAR Calculations in an Anatomically Based Realistic Model of the Head for Mobile Communication Transceivers at 900 MHz and 1.8 GHz," Physics in Medicine and Biology, Vol. 39, pp. 1537-1553, 1994.

[5] O.P. Gandhi, J.Y. Chen, "Numerical Dosimetry at Power Line Frequencies Using Anatomically-Based Models," Bioelectromagnetics Supplement 1992, pp. 43-60

[6] C. M. Furse, J. Y. Chen, and O. P. Gandhi, "Calculation of Electric Fields and Currents Induced in a Millimeter-Resolution Human Model at 60 Hz Using the FDTD Method," Bioelectromagnetics, 19(5), 1998, pp.293-299

[7] O. P. Gandhi, Y. G. Gu, J. Y. Chen, and H. I. Bassen, "Specific Absorption Rates and Induced Current Distributions in an Anatomically Based Human Model for Plane-Wave Exposure," Health Physics, Vol. 63, pp. 281-290, 1992.

[8] G.Lazzi, S.S. Pattnaik, C.M. Furse, O.P. Gandhi, "Comparison of FDTD-Computed and Measured Radiation Patterns of Commercial Mobile Telephones in Presence of the Human Head," IEEE Trans. Antennas and Propagation, June 1998, pp.943-944

[9] A. Taflove, K. Umashankar, "Review of FD-TD Numerical Modeling of Electromagnetic Wave Scattering and Radar Cross Section," Proc. IEEE, Vol.77, pp. 682-698, May 1989

[10] T. Shibata, T. Hayashi, T. Kimura, "Analysis of Microstrip Circuits Using Three-Dimensional Full-Wave Electromagnetic Field Analysis in the Time Domain," IEEE Trans. Microwave Theory and Techniques, June 1988, pp. 1064-1070

[11] J.C. Olivier, "Mutual Coupling Between Waveguide Apertures Mounted on a Common Conducting Surface Using a Time- and Fourier-Gated Pulsed FDTD Method," IEEE Trans. Microwave Theory and Techniques, Feb. 1993, pp. 290-297

[12] A.C. Cangellaris, M. Gribbons, G. Sohos, "A Hybrid Spectral/FDTD Method for the Electromagnetic Analysis of Guided Wave Structures," IEEE Microwave and Guided Wave Letters, Oct. 1993, pp. 375-377

[13] C.M. Furse, S.P. Mathur, O.P. Gandhi, "Improvements to the Finite-Difference Time-Domain Method for Calculating the Radar Cross Section of a Perfectly Conducting Target," IEEE Trans. Microwave Theory and Techniques, Vol. MTT-38, No. 7, July 1990, pp. 919-927

[14] Z. Bi, Y.Shen, K.Wu, J.Litva, "Fast Finite-Difference Time-Domain Analysis of Resonators Using Digital Filtering and Spectrum Estimation Techniques," IEEE Trans. Microwave Theory and Techniques, pp. 1611-1619, 1992

[15] C.M. Furse, "Use of the Finite Difference Time Domain Method for Broad Band Calculations of Electromagnetic Scattering and Absorption from Large Heterogeneous Objects," Ph.D. dissertation, University of Utah, 1994

[16] A.Taflove, Computational Electrodynamics: The Finite-Difference Time-Domain Method, Artech House, 1995

[17] K.S. Kunz, R.J. Luebbers, The Finite Difference Time Domain Method for Electromagnetics, CRC Press, Boca Raton, FL, 1993

[18] S. Haykin, Digital Communication, John Wiley and Sons, 1988

[19] C.M. Furse, O.P. Gandhi, "Why the DFT is faster than the FFT for time-to-frequency domain conversion," IEEE Microwave and Guided Wave Letters , Vol. 6, No. 10, 1995, pp. 326-328

[20] A. Dutt and V. Kokhlin, "Fast Fourier Transforms for non-equispaced data," SIAM J. Sci. Comput., Vol. 14, pp. 1368-1393, 1993

[21] C.M. Furse, "Faster than Fourier -- Ultra-Efficient Time-to-Frequency Domain Conversions to FDTD Applied to Bioelectromagnetic Dosimetry," ACES Symposium (Dec. 3, 1997) , March 16-20, 1998, Monterey, CA

[22] C.M. Furse, D.H. Roper, D.N. Buechler, D.A. Christensen, C.H. Durney, "The Problems and Treatment of DC Offsets in FDTD Simulations," IEEE Transactions on Antennas and Propagation, October 2000

[23] D.S. Katz, E.T. Thiele, A. Taflove, “Validation and Extension to Three Dimensions of the Berenger PML Absorbing Boundary Condition for FD-TD Meshes,” IEEE Microwave and Guided Wave Letters , 4(8), pp. 268- 270, August, 1994

[24] Buechler DN, Roper DH, Christensen DA, Durney CH (1995): Modeling sources in the FDTD formulation and their use in quantifying source and boundary condition errors. IEEE Trans. Microwave Theory and Techniques 43(4).

[25] A. Ralston, P. Rabinowitz, "A First Course in Numerical Analysis," McGraw-Hill, 1978, p.417

[26] G.H. Golub, C.F. Van Loan, Matrix Computations, second edition, Johns Hopkins University Press, 1989, p. 239

[27] J. Van Bladel, Electromagnetic Fields, Hemisphere Publishing Co., 1985, pp. 254-258

[28] A.Taflove, editor, Advances in Computational Electrodynamics, Artech House, 1998

[29] T.Wang, and G.W.Hohmann, "A finite-difference time-domain solution for three- dimensional electromagnetic modeling," Geophysics, 58, 797-809, 1993

[30] J.Y.Chen and O.P. Gandhi OP, "RF currents induced in an anatomically-based model of a human for plane-wave exposures 20-100 MHz," Health Physics, Vol. 57, pp. 89-98, 1989

[31] T. Dawson, K. Caputa, M.A. Stuchly, "High-resolution organ dosimetry for human exposure to low-frequency electric fields," IEEE Trans. Power Delivery, accepted for publication

[32] D.Johnson, C.Furse, A.C.Tripp, "FDTD Modeling of the Borehole EM Response of a Conductive Ore Deposit in a Lossy Dielectric," Society of Exploration Geophysics International Conference, Sept. 12-15, 1998, New Orleans, LA

[33] M. R. Zunoubi, N. H. Younan, J. H. Beggs, and C. D. Taylor, "FDTD Analysis of Linear Antennas Driven From a Discrete Impulse Excitation," IEEE Trans.Electromagn. Compat., vol. 39, pp. 247-250, Aug. 1997.