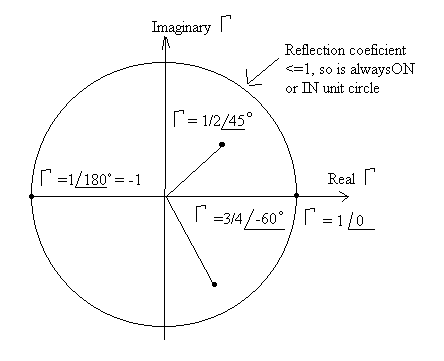
ECE 6130 Lecture 4: SMITH CHARTS
Text Section: 2.4
Portfolio Question:
1) Describe and Demonstrate how to use a Smith Chart to find impedance, Vmin, Vmax, SWR, reflection coefficient, etc.
See Chapter 2, Problems 7-12
Smith Chart Circles:
A Smith chart is a graphical representation of the complex reflection coefficient, G
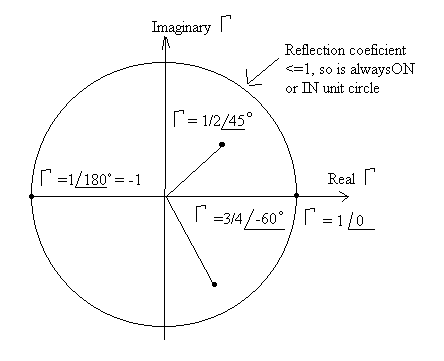
Smith Chart for Reflection Coefficient and Load Impedance:
Reflection Coefficient and Load (ZL) are directly related:
G = (ZL / Zo - 1) / (ZL/Zo+ 1) = (zL - 1) / (zL + 1)
OR
ZL / Zo = zL = (1 + G ) / (1 - G ) ß This is NORMALIZED load impedance
zL = rL + j xL
The real and imaginary parts of zL are functions of G , and these functions can be plotted on the same chart. Remember |G | £ 1.
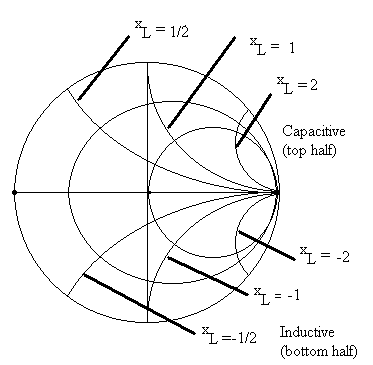
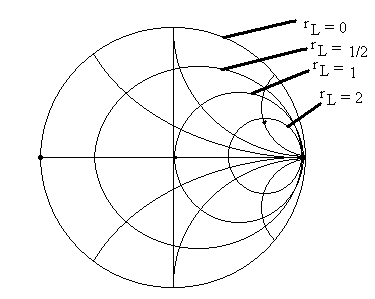
Example: Given ZL , find G using Smith Chart
See transparencies (Copies to be made available in copy room)
How to find G :
1) Find Normalized load Impedance, zL = ZL / Zo = rL + j xL
Zo = 100 ohms
ZL = open circuit
G =1 Ð 0 (which is what we expect for an open circuit)
ZL = open circuit
G =1 Ð 180° = -1 (which is what we expect for an short circuit)
ZL = 100 + j 0 ohms
G =0 Ð ? (which is what we expect for a matched load)
ZL = 100 + j 100 ohms
G =0.45 Ð 63°
G = (zL - 1) / (zL + 1) = (0+j1) / (2+j1) =1Ð 90° / 2.236 Ð 26.56 ° = 0.45 Ð 63.43°
How do you find load impedance if given G ?
Admittance vs. Impedance:
Admittance yL = 1 / zL
G = (zL - 1) / (zL + 1) = (1/yL - 1) / (1/yL + 1) = - (yL - 1) / (yL + 1) = 180 out of phase
Steps to find G from yL:
EXAMPLE (See transparencies)
Input Impedance:
Zin = Zo [1 + G e -jb l ] / [1 - G e -jb l ]
zin = Zin / Zo = [1 + G e -j2b l ] / [1 - G e -j2b l ]
Define reflection coefficient at the input (NOT G g ) as the reflection coefficient looking into the load frm the input location. G l = G L Ð -2b l
This represents moving 2b l radians towards the generator.
You can convert this distance to degrees, and read it off the outer circles on the Smith Chart (notice DIRECTION to the generator is marked)
OR 2b l = 2(2p / l ) l = 4p (l / l ) This has been normalized for you on the outside circle around the Smith Chart. Observe that if l=l , this represents 2 complete rotations around the Smith Chart. L = l /2 represents one complete rotation.
Does this make sense? For a Transmission line of length L = l /2, traveling from generator to the load and back would represent a phase shift of 360 degrees … one complete rotation.
Then zin = [1 + G l] / [1 - G l ]
How to find Zin :
EXAMPLE (see transparencies)
Standing Wave Ratio:
To read SWR from the Smith Chart:
EXAMPLE (See transparencies)
Voltage Minima and Maxima:
To read Voltage maxima off Smith Chart:
EXAMPLE (See transparencies)