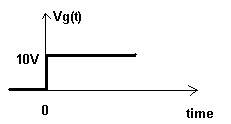Open Notes, Open Book.
- (25 points) For the transmission line shown below:
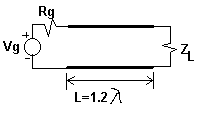 Find the input impedance to the line. Zin = _________________
Find the input impedance to the line. Zin = _________________
- Find the reflection coefficient of the load. G
L = __________________
- Find the VSWR = ______________
Plot the envelope of the standing wave on the line as a function of z. Clearly show the locations of the voltage minima and maxima, and their relative heights.
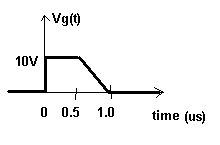
(d) Given Vg = 10.0 sin (w
t) Volts, write expressions for Vo+ and Vo-
- (25 points) For the transmission line shown below Rg = 100 ohms, ZL = 25 ohms, Zo = 50 ohms, Length = 300 meters.
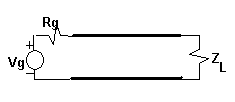
- Plot the voltage on the line at the center of the line (z=150m) as a function of time for 4 m
s for the generator voltage shown below.
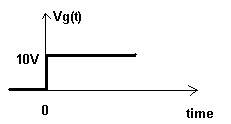
(b) Plot the current at the load as a function of time for 4 m
s.
- Plot the voltage on the line as a function of distance at time t=2.5 m
s.
- Repeat part (a) for the generator voltage ( pulse wave form )shown below.
- (25 points) An RG 58 coaxial transmission line is used to transmit binary data at 1 GHz. The data pulses are 5 V peak, and the detector at the end will register a binary value of "1" when the received voltage is greater than or equal to 3.6 V.
Information about RG 58 coaxial line: a = 0.89 mm, b = 3.53 mm, filled with polyethylene with e
r = 2.26, loss tangent = 0.00031 . [e
'' = e
o e
r * losstan]. Conductors are made of copper.
- What are the values of R', L', C', G' for this cable?
- What is the longest cable that can be used to send these signals accurately?
- What will be the magnitude of the 5 V signal after it has propagated 10 meters down the line?
- How long will it take for the wave to propagate 10 meters down the line?
- (25 points) For a rectangular transmission line shown below, the following fields are observed:
Ey = K a sin (mp
x / a)
Hx = - Ey b
/ (w
m
)
(K is a constant.)
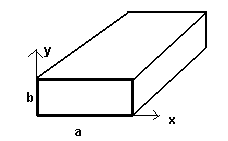
Write the integral equations to find R,L,G,C for this transmission line.
Name ________________________________
Problem 1 ___________ / 25 points
Problem 2 ___________ / 25 points
Problem 3 ___________ / 25 points
Problem 4 ___________ / 25 points
Total ___________ / 100 points
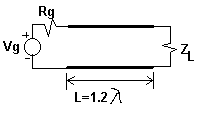 Find the input impedance to the line. Zin = _________________
Find the input impedance to the line. Zin = _________________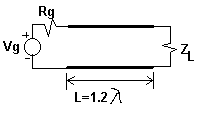 Find the input impedance to the line. Zin = _________________
Find the input impedance to the line. Zin = _________________